Lösung 2.1:4e
Aus Online Mathematik Brückenkurs 2
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 8: | Zeile 8: | ||
<math>x=a</math> and <math>x=b</math>, between the line and the parabola, we can calculate the area as the integral of the difference between the curves' ''y''-values, | <math>x=a</math> and <math>x=b</math>, between the line and the parabola, we can calculate the area as the integral of the difference between the curves' ''y''-values, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\text{Area} = \int\limits_a^b \bigl(x+2-x^2\bigr)\,dx\,\textrm{.}</math>}} |
The curves' points of intersection are those points which lie on both curves, i.e. which satisfy both curves' equations | The curves' points of intersection are those points which lie on both curves, i.e. which satisfy both curves' equations | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\left\{\begin{align} |
y &= x+2\,,\\[5pt] | y &= x+2\,,\\[5pt] | ||
y &= x^2\,\textrm{.} | y &= x^2\,\textrm{.} | ||
| Zeile 19: | Zeile 19: | ||
By eliminating <math>y</math>, we obtain an equation for <math>x</math>, | By eliminating <math>y</math>, we obtain an equation for <math>x</math>, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>x^{2}=x+2\,\textrm{.}</math>}} |
If we move all ''x''-terms to the left-hand side, | If we move all ''x''-terms to the left-hand side, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>x^2-x=2\,,</math>}} |
and complete the square, we obtain | and complete the square, we obtain | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
\Bigl(x-\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 &= 2\\[5pt] | \Bigl(x-\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 &= 2\\[5pt] | ||
\Bigl(x-\frac{1}{2}\Bigr)^2 &= \frac{9}{4}\,\textrm{.} | \Bigl(x-\frac{1}{2}\Bigr)^2 &= \frac{9}{4}\,\textrm{.} | ||
| Zeile 36: | Zeile 36: | ||
The area of the region is now given by | The area of the region is now given by | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
\text{Area} | \text{Area} | ||
&= \int\limits_{-1}^2 \bigl(x+2-x^2\bigr)\,dx\\[5pt] | &= \int\limits_{-1}^2 \bigl(x+2-x^2\bigr)\,dx\\[5pt] | ||
Version vom 13:00, 10. Mär. 2009
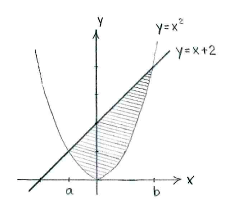
The double inequality means that we look for the area of the region which is bounded above in the y-direction by the straight line \displaystyle y=x+2 and from below by the parabola \displaystyle y=x^2.
If we sketch the line and the parabola, the region is given by the region shaded in the figure below.
As soon as we have determined the x-coordinates of the points of intersection, \displaystyle x=a and \displaystyle x=b, between the line and the parabola, we can calculate the area as the integral of the difference between the curves' y-values,
| \displaystyle \text{Area} = \int\limits_a^b \bigl(x+2-x^2\bigr)\,dx\,\textrm{.} |
The curves' points of intersection are those points which lie on both curves, i.e. which satisfy both curves' equations
| \displaystyle \left\{\begin{align}
y &= x+2\,,\\[5pt] y &= x^2\,\textrm{.} \end{align} \right. |
By eliminating \displaystyle y, we obtain an equation for \displaystyle x,
| \displaystyle x^{2}=x+2\,\textrm{.} |
If we move all x-terms to the left-hand side,
| \displaystyle x^2-x=2\,, |
and complete the square, we obtain
| \displaystyle \begin{align}
\Bigl(x-\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 &= 2\\[5pt] \Bigl(x-\frac{1}{2}\Bigr)^2 &= \frac{9}{4}\,\textrm{.} \end{align} |
Taking the root then gives that \displaystyle x=\tfrac{1}{2}\pm \tfrac{3}{2}. In other words, \displaystyle x=-1 and \displaystyle x=2\,.
The area of the region is now given by
| \displaystyle \begin{align}
\text{Area} &= \int\limits_{-1}^2 \bigl(x+2-x^2\bigr)\,dx\\[5pt] &= \Bigl[\ \frac{x^2}{2} + 2x - \frac{x^3}{3}\ \Bigr]_{-1}^2\\[5pt] &= \frac{2^2}{2} + 2\cdot 2 - \frac{2^3}{3} - \Bigl( \frac{(-1)^2}{2} + 2\cdot (-1) - \frac{(-1)^3}{3}\Bigr)\\[5pt] &= 2 + 4 - \frac{8}{3} - \frac{1}{2} + 2 - \frac{1}{3}\\[5pt] &= \frac{9}{2}\,\textrm{.} \end{align} |