Lösung 1.3:1d
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
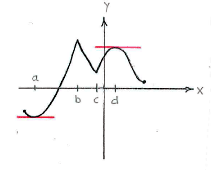
| - | The function has critical points at the points | + | The function has critical points at the points <math>x=a</math> and <math>x=d</math>, (see figure below), i.e. the derivatives are equal to zero, but note that <math>x=b</math> and <math>x=c</math> are not critical points (the derivative is not even defined at these points). |
| - | <math>x=a</math> | + | |
| - | and | + | |
| - | <math>x=d</math>, (see figure below), i.e. the derivatives are equal to zero, but note that | + | |
| - | <math>x=b</math> | + | |
| - | and | + | |
| - | <math>x=c</math> | + | |
| - | are not critical points (the derivative is not even defined at these points). | + | |
[[Image:1_3_1_d1.gif|center]] | [[Image:1_3_1_d1.gif|center]] | ||
| - | The function has local minimum points at | + | The function has local minimum points at <math>x=a</math>, <math>x=c</math> and the right endpoint of the interval of definition and the local maximum points at the left endpoint, <math>x=b</math>, and <math>x=d</math>. Of these, <math>x=b</math> is the global maximum and <math>x=a</math> is the global minimum. |
| - | <math>x=a</math>, | + | |
| - | <math>x=c</math> | + | |
| - | and the right endpoint of the interval of definition and the local maximum points at the left endpoint, | + | |
| - | <math>x=b</math>, and | + | |
| - | <math>x=d</math>. Of these, | + | |
| - | <math>x=b</math> | + | |
| - | is the global maximum and | + | |
| - | <math>x=a</math> | + | |
| - | is the global minimum. | + | |
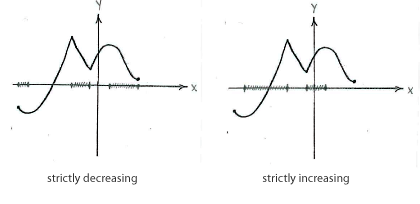
Between the local extreme points, the function is strictly increasing or decreasing. | Between the local extreme points, the function is strictly increasing or decreasing. | ||
| - | |||
[[Image:1_3_1_d2.gif|center]] | [[Image:1_3_1_d2.gif|center]] | ||
Version vom 12:05, 17. Okt. 2008
The function has critical points at the points \displaystyle x=a and \displaystyle x=d, (see figure below), i.e. the derivatives are equal to zero, but note that \displaystyle x=b and \displaystyle x=c are not critical points (the derivative is not even defined at these points).
The function has local minimum points at \displaystyle x=a, \displaystyle x=c and the right endpoint of the interval of definition and the local maximum points at the left endpoint, \displaystyle x=b, and \displaystyle x=d. Of these, \displaystyle x=b is the global maximum and \displaystyle x=a is the global minimum.
Between the local extreme points, the function is strictly increasing or decreasing.