Lösung 3.2:1b
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
| - | {{NAVCONTENT_START}} | ||
We can easily calculate <math>z+u</math> and <math>z-u</math>, | We can easily calculate <math>z+u</math> and <math>z-u</math>, | ||
| - | <math>\begin{align}z+u&=2+i+(-1-2i)=2-1+(1-2)i=1-i,\\ | + | {{Displayed math||<math>\begin{align} |
| - | z-u&=2+i-(-1-2i)=2+1+(1+2)i=3+3i,\end{align}</math> | + | z+u &= 2+i+(-1-2i) = 2-1+(1-2)i = 1-i,\\[5pt] |
| + | z-u &= 2+i-(-1-2i) = 2+1+(1+2)i = 3+3i, | ||
| + | \end{align}</math>}} | ||
and then mark them on the complex plane. | and then mark them on the complex plane. | ||
| Zeile 15: | Zeile 16: | ||
[[Image:3_2_1_b2.gif|center]] | [[Image:3_2_1_b2.gif|center]] | ||
| - | or interpret | + | or interpret <math>z-u</math> from the vector relation |
| - | <math>z=(z-u)+u</math> | + | {{Displayed math||<math>z=(z-u)+u\,,</math>}} |
i.e. <math>z-u</math> is the vector we add to <math>u</math> to arrive at <math>z</math>. | i.e. <math>z-u</math> is the vector we add to <math>u</math> to arrive at <math>z</math>. | ||
[[Image:3_2_1_b3.gif|center]] | [[Image:3_2_1_b3.gif|center]] | ||
| - | |||
| - | {{NAVCONTENT_STOP}} | ||
Version vom 09:21, 29. Okt. 2008
We can easily calculate \displaystyle z+u and \displaystyle z-u,
| \displaystyle \begin{align}
z+u &= 2+i+(-1-2i) = 2-1+(1-2)i = 1-i,\\[5pt] z-u &= 2+i-(-1-2i) = 2+1+(1+2)i = 3+3i, \end{align} |
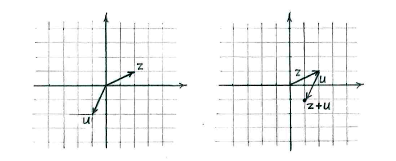
and then mark them on the complex plane.
An alternative is to view \displaystyle z and \displaystyle u as vectors and \displaystyle z+u as a vector addition of \displaystyle z and \displaystyle u.
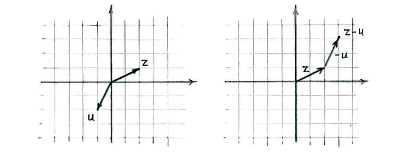
We can either view the vector subtraction \displaystyle z-u as \displaystyle z+(-u),
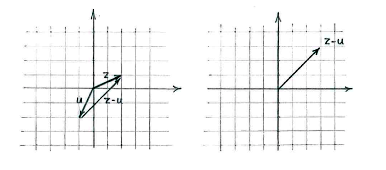
or interpret \displaystyle z-u from the vector relation
| \displaystyle z=(z-u)+u\,, |
i.e. \displaystyle z-u is the vector we add to \displaystyle u to arrive at \displaystyle z.