Lösung 3.3:2b

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 3.3:2b moved to Solution 3.3:2b: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
The The equation
-
<center> [[Image:3_3_2b-1(2).gif]] </center>
+
<math>z^{3}=-\text{1 }</math>
-
{{NAVCONTENT_STOP}}
+
is a so-called binomial equation, which we solve by writing both sides in polar form. We have
-
{{NAVCONTENT_START}}
+
 
-
<center> [[Image:3_3_2b-2(2).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
<math>\begin{align}
 +
& z=r\left( \cos \alpha +i\sin \alpha \right) \\
 +
& -1=1\left( \cos \pi +i\sin \pi \right) \\
 +
\end{align}</math>
 +
 
 +
 
 +
and, with the help of de Moivre's formula, the equation becomes
 +
 
 +
 
 +
<math>r^{3}\left( \cos 3\alpha +i\sin 3\alpha \right)=1\left( \cos \pi +i\sin \pi \right)</math>
 +
 
 +
 
 +
Both sides are equal when their magnitudes are equal and the arguments differ by a multiple of
 +
<math>2\pi </math>,
 +
 
 +
 
 +
<math>\left\{ \begin{array}{*{35}l}
 +
r^{3}=1 \\
 +
3\alpha =\pi +2n\pi \quad \left( n\text{ an arbitrary integer} \right)\text{ } \\
 +
\end{array} \right.</math>
 +
 +
which gives that
 +
 
 +
 
 +
<math>\left\{ \begin{array}{*{35}l}
 +
r=1 \\
 +
\alpha =\frac{\pi }{3}+\frac{2n\pi }{3}\quad \left( n\text{ an arbitrary integer} \right)\text{ } \\
 +
\end{array} \right.</math>
 +
 
 +
 
 +
 
 +
For every third integer
 +
<math>n</math>, the solution formula gives in principal the same value for the argument (the difference is a multiple of
 +
<math>2\pi </math>), so the equation has in reality three solutions (for
 +
<math>n=0,\ 1</math>
 +
and
 +
<math>\text{2}</math>):
 +
 
 +
 
 +
<math>z=\left\{ \begin{array}{*{35}l}
 +
1\centerdot \left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right) \\
 +
1\centerdot \left( \cos \pi +i\sin \pi \right) \\
 +
1\centerdot \left( \cos \frac{5\pi }{3}+i\sin \frac{5\pi }{3} \right) \\
 +
\end{array} \right.=\left\{ \begin{array}{*{35}l}
 +
\frac{1+i\sqrt{3}}{2} \\
 +
-1 \\
 +
\frac{1-i\sqrt{3}}{2} \\
 +
\end{array} \right.</math>
 +
 
 +
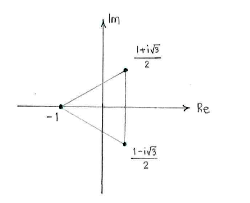
We obtain the typical behaviour that the solutions are corner points in a regular polygon (a triangle in this case because the degree of the equation is
 +
<math>\text{3}</math>).
 +
 
 +
 
[[Image:3_3_2_b.gif|center]]
[[Image:3_3_2_b.gif|center]]

Version vom 10:01, 24. Okt. 2008

The The equation \displaystyle z^{3}=-\text{1 } is a so-called binomial equation, which we solve by writing both sides in polar form. We have


\displaystyle \begin{align} & z=r\left( \cos \alpha +i\sin \alpha \right) \\ & -1=1\left( \cos \pi +i\sin \pi \right) \\ \end{align}


and, with the help of de Moivre's formula, the equation becomes


\displaystyle r^{3}\left( \cos 3\alpha +i\sin 3\alpha \right)=1\left( \cos \pi +i\sin \pi \right)


Both sides are equal when their magnitudes are equal and the arguments differ by a multiple of \displaystyle 2\pi ,


\displaystyle \left\{ \begin{array}{*{35}l} r^{3}=1 \\ 3\alpha =\pi +2n\pi \quad \left( n\text{ an arbitrary integer} \right)\text{ } \\ \end{array} \right.

which gives that


\displaystyle \left\{ \begin{array}{*{35}l} r=1 \\ \alpha =\frac{\pi }{3}+\frac{2n\pi }{3}\quad \left( n\text{ an arbitrary integer} \right)\text{ } \\ \end{array} \right.


For every third integer \displaystyle n, the solution formula gives in principal the same value for the argument (the difference is a multiple of \displaystyle 2\pi ), so the equation has in reality three solutions (for \displaystyle n=0,\ 1 and \displaystyle \text{2}):


\displaystyle z=\left\{ \begin{array}{*{35}l} 1\centerdot \left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right) \\ 1\centerdot \left( \cos \pi +i\sin \pi \right) \\ 1\centerdot \left( \cos \frac{5\pi }{3}+i\sin \frac{5\pi }{3} \right) \\ \end{array} \right.=\left\{ \begin{array}{*{35}l} \frac{1+i\sqrt{3}}{2} \\ -1 \\ \frac{1-i\sqrt{3}}{2} \\ \end{array} \right.

We obtain the typical behaviour that the solutions are corner points in a regular polygon (a triangle in this case because the degree of the equation is \displaystyle \text{3}).


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.3:2b“