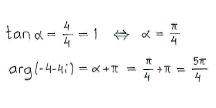Lösung 3.2:6c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 3.2:6c moved to Solution 3.2:6c: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
We need to know the number's magnitude and argument, in order to be able to write down its polar form.
-
<center> [[Image:3_2_6c.gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
We obtain the number's magnitude as its distance to the origin; it is obtained by the distance formula:
 +
 
 +
 
 +
<math>\left| -4-4i \right|=\sqrt{\left( -4 \right)^{2}+\left( -4 \right)^{2}}=\sqrt{16+16}=\sqrt{16\centerdot 2}=4\sqrt{2}</math>
 +
 
 +
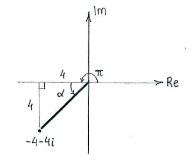
Furthermore, the number lies in the third quadrant (negative real and imaginary parts) and if we introduce an auxiliary triangle in that quadrant, we can determine the angle that the number makes with the negative real axis. Then, we get the number's argument by adding the angle
 +
<math>\pi </math>.
 +
 
[[Image:3_2_6_c1.gif]] [[Image:3_2_6_c2.gif]]
[[Image:3_2_6_c1.gif]] [[Image:3_2_6_c2.gif]]
<!-- texten är i en bild och figuern i en... -->
<!-- texten är i en bild och figuern i en... -->
 +
 +
The number's polar form is thus
 +
 +
 +
<math>4\sqrt{2}\left( \cos \frac{5\pi }{4}+i\sin \frac{5\pi }{4} \right)</math>

Version vom 10:22, 23. Okt. 2008

We need to know the number's magnitude and argument, in order to be able to write down its polar form.

We obtain the number's magnitude as its distance to the origin; it is obtained by the distance formula:


\displaystyle \left| -4-4i \right|=\sqrt{\left( -4 \right)^{2}+\left( -4 \right)^{2}}=\sqrt{16+16}=\sqrt{16\centerdot 2}=4\sqrt{2}

Furthermore, the number lies in the third quadrant (negative real and imaginary parts) and if we introduce an auxiliary triangle in that quadrant, we can determine the angle that the number makes with the negative real axis. Then, we get the number's argument by adding the angle \displaystyle \pi .


Image:3_2_6_c1.gif Image:3_2_6_c2.gif

The number's polar form is thus


\displaystyle 4\sqrt{2}\left( \cos \frac{5\pi }{4}+i\sin \frac{5\pi }{4} \right)

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:6c“