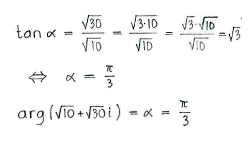Lösung 3.2:6d

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
(Ny sida: {{NAVCONTENT_START}} <center> Bild:3_2_6d.gif </center> {{NAVCONTENT_STOP}})
Aktuelle Version (13:10, 13. Mai 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 7 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
Wir berechnen zuerst den Betrag der komplexen Zahl,
-
<center> [[Bild:3_2_6d.gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
{{Abgesetzte Formel||<math>\begin{align}
 +
\bigl|\sqrt{10}+\sqrt{30}i\bigr|
 +
&= \sqrt{\bigl(\sqrt{10}\,\bigr)^2+\bigl(\sqrt{30}\,\bigr)^2}\\[5pt]
 +
&= \sqrt{10+30}\\[5pt]
 +
&= \sqrt{40}\\[5pt]
 +
&= \sqrt{4\cdot 10}\\[5pt]
 +
&= 2\sqrt{10}\,\textrm{.}
 +
\end{align}</math>}}
 +
 
 +
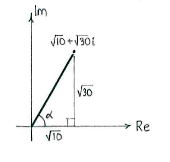
Nachdem die Zahl im ersten Quadrant liegt, erhalten wir das Argument durch einfache Trigonometrie.
 +
 
 +
[[Image:3_2_6_d_bild.gif]] [[Image:3_2_6_d_bildtext.gif]]
 +
 
 +
Die Polarform ist also
 +
 
 +
{{Abgesetzte Formel||<math>2\sqrt{10}\Bigl( \cos\frac{\pi}{3} + i\sin\frac{\pi}{3} \Bigr)\,\textrm{.}</math>}}

Aktuelle Version

Wir berechnen zuerst den Betrag der komplexen Zahl,

\displaystyle \begin{align}

\bigl|\sqrt{10}+\sqrt{30}i\bigr| &= \sqrt{\bigl(\sqrt{10}\,\bigr)^2+\bigl(\sqrt{30}\,\bigr)^2}\\[5pt] &= \sqrt{10+30}\\[5pt] &= \sqrt{40}\\[5pt] &= \sqrt{4\cdot 10}\\[5pt] &= 2\sqrt{10}\,\textrm{.} \end{align}

Nachdem die Zahl im ersten Quadrant liegt, erhalten wir das Argument durch einfache Trigonometrie.

Image:3_2_6_d_bild.gif Image:3_2_6_d_bildtext.gif

Die Polarform ist also

\displaystyle 2\sqrt{10}\Bigl( \cos\frac{\pi}{3} + i\sin\frac{\pi}{3} \Bigr)\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:6d“