Lösung 3.2:2e
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
K (Robot: Automated text replacement (-ä +ä)) |
K (Robot: Automated text replacement (-ö +ö)) |
||
| Zeile 14: | Zeile 14: | ||
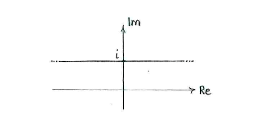
daher ist <math>y=1</math>. | daher ist <math>y=1</math>. | ||
| - | Also besteht unsere | + | Also besteht unsere Lösungsmege aus allen komlexen Zahlen deren Imaginärteil 1 ist. |
[[Image:3_2_2_e.gif|center]] | [[Image:3_2_2_e.gif|center]] | ||
Aktuelle Version
Wir schreiben die gesuchte komplexe Zahl \displaystyle z mit ihrem Realteil und Imaginärteil. Nach Aufgabenstellung ist der Realteil \displaystyle x , den unbekannten Imaginärteil nennen wir \displaystyle y .
| \displaystyle z = x + i y . |
Es soll also gelten
| \displaystyle x = i + \overline{z} = i + (x -iy) = x + i (1-y) . |
Also soll gelten
| \displaystyle x = x + i (1-y) |
und das ist äquivalent zu
| \displaystyle 0 = i (1-y) . |
daher ist \displaystyle y=1.
Also besteht unsere Lösungsmege aus allen komlexen Zahlen deren Imaginärteil 1 ist.