Lösung 1.3:2b
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
| (Der Versionsvergleich bezieht 2 dazwischen liegende Versionen mit ein.) | |||
| Zeile 1: | Zeile 1: | ||
| - | Lokale | + | Lokale Extremstellen einer Funktion sind entweder: |
| - | # stationäre | + | # stationäre Stellen mit <math>f^{\,\prime}(x)=0</math>, |
| - | # Singuläre | + | # Singuläre Stellen, in denen die Funktion nicht differenzierbar ist, oder |
| - | # | + | # Randstellen. |
Wir untersuchen alle drei Fälle: | Wir untersuchen alle drei Fälle: | ||
| Zeile 15: | Zeile 15: | ||
<li>Da die Funktion ein Polynom ist, ist sie überall differenzierbar.</li> | <li>Da die Funktion ein Polynom ist, ist sie überall differenzierbar.</li> | ||
| - | <li>Die Funktion ist überall definiert, also hat unser Intervall keine | + | <li>Die Funktion ist überall definiert, also hat unser Intervall keine Randstellen.</li> |
</ol> | </ol> | ||
| - | Also sind alle lokalen | + | Also sind alle lokalen Extremstellen auch stationäre Stellen. Somit ist <math>x=3/2\,</math> die einzige Stelle, die eine Extremstelle sein könnte. Mit einer Vorzeichentabelle untersuchen wir, ob die Stelle eine Extremstelle ist. |
| Zeile 39: | Zeile 39: | ||
|} | |} | ||
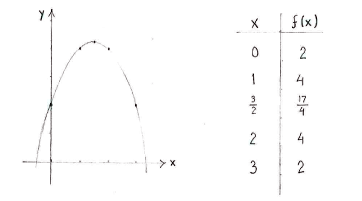
| - | Da die Funktion eine quadratische Funktion ist, ist deren Graph eine Parabel mit | + | Da die Funktion eine quadratische Funktion ist, ist deren Graph eine Parabel mit dem Maximum <math> \frac{17}{4} </math> an der Stelle <math> x = \frac{3}{2} </math>. |
[[Image:1_3_2_b.gif||center]] | [[Image:1_3_2_b.gif||center]] | ||
Aktuelle Version
Lokale Extremstellen einer Funktion sind entweder:
- stationäre Stellen mit \displaystyle f^{\,\prime}(x)=0,
- Singuläre Stellen, in denen die Funktion nicht differenzierbar ist, oder
- Randstellen.
Wir untersuchen alle drei Fälle:
- Die Ableitung von \displaystyle f(x) ist
und wird null für \displaystyle x=3/2\,.\displaystyle f^{\,\prime}(x) = 3-2x - Da die Funktion ein Polynom ist, ist sie überall differenzierbar.
- Die Funktion ist überall definiert, also hat unser Intervall keine Randstellen.
Also sind alle lokalen Extremstellen auch stationäre Stellen. Somit ist \displaystyle x=3/2\, die einzige Stelle, die eine Extremstelle sein könnte. Mit einer Vorzeichentabelle untersuchen wir, ob die Stelle eine Extremstelle ist.
| \displaystyle x | \displaystyle \tfrac{3}{2} | ||
| \displaystyle f^{\,\prime}(x) | \displaystyle + | \displaystyle 0 | \displaystyle - |
| \displaystyle f(x) | \displaystyle \nearrow | \displaystyle \tfrac{17}{4} | \displaystyle \searrow |
Da die Funktion eine quadratische Funktion ist, ist deren Graph eine Parabel mit dem Maximum \displaystyle \frac{17}{4} an der Stelle \displaystyle x = \frac{3}{2} .