Aus Online Mathematik Brückenkurs 2

Version vom 09:22, 7. Apr. 2008 (bearbeiten) Oskar (Diskussion | Beiträge) (Ny sida: {{NAVCONTENT_START}} <center> Bild:2_2_2a-1(2).gif </center> {{NAVCONTENT_STOP}} {{NAVCONTENT_START}} <center> Bild:2_2_2a-1(2).gif </center> {{NAVCONTENT_STOP}}) ← Zum vorherigen Versionsunterschied		Aktuelle Version (12:10, 27. Aug. 2009) (bearbeiten) (rückgängig) Sekretariat1 (Diskussion | Beiträge)
(Der Versionsvergleich bezieht 9 dazwischen liegende Versionen mit ein.)
Zeile 1:		Zeile 1:
-	{{NAVCONTENT_START}}	+	Wenn wir die Substition <math>u=5x</math> ausführen, erhalten wir ein schon bekanntes Integral.
-	<center> [[Bild:2_2_2a-1(2).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	{{Abgesetzte Formel||<math>\int\limits_0^{\pi} \cos 5x\,dx = \left\{\begin{align}
-	{{NAVCONTENT_START}}	+	u &= 5x\\[5pt]
-	<center> [[Bild:2_2_2a-1(2).gif]] </center>	+	du &= (5x)'\,dx = 5\,dx
-	{{NAVCONTENT_STOP}}	+	\end{align}\right\} = \frac{1}{5}\int\limits_0^{5\pi} \cos u\,du</math>}}
		+
		+	Hier haben wir <math>dx</math> mit <math>\tfrac{1}{5}\,du</math> ersetzt. Die Grenzen, die wir erhalten sind <math>u=5\cdot 0=0</math>
		+	und <math>u=5\cdot \pi = 5\pi\,</math>.
		+
		+	Wir erhalten das Integral
		+
		+	{{Abgesetzte Formel||<math>\frac{1}{5}\int\limits_0^{5\pi} \cos u\,du = \frac{1}{5}\Bigl[\ \sin u\ \Bigr]_0^{5\pi} = \frac{1}{5}( \sin 5\pi -\sin 0) = \frac{1}{5}(0-0) = 0\,\textrm{.}</math>}}
		+
		+
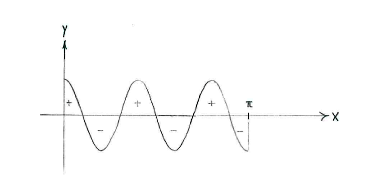
		+	Hinweis: Zeichnen wir die Graphe von <math>y=\cos 5x</math>, sehen wir, dass die gesamte Fläche oberhalb der ''x''-Achse genauso groß ist wie die gesamte Fläche unterhalb der ''x''-Achse ist.
		+
		+	[[Image:2_2_2_a.gif|center]]

---

Aktuelle Version

Wenn wir die Substition \displaystyle u=5x ausführen, erhalten wir ein schon bekanntes Integral.

\displaystyle \int\limits_0^{\pi} \cos 5x\,dx = \left\{\begin{align} u &= 5x\\[5pt] du &= (5x)'\,dx = 5\,dx \end{align}\right\} = \frac{1}{5}\int\limits_0^{5\pi} \cos u\,du

Hier haben wir \displaystyle dx mit \displaystyle \tfrac{1}{5}\,du ersetzt. Die Grenzen, die wir erhalten sind \displaystyle u=5\cdot 0=0 und \displaystyle u=5\cdot \pi = 5\pi\,.

Wir erhalten das Integral

\displaystyle \frac{1}{5}\int\limits_0^{5\pi} \cos u\,du = \frac{1}{5}\Bigl[\ \sin u\ \Bigr]_0^{5\pi} = \frac{1}{5}( \sin 5\pi -\sin 0) = \frac{1}{5}(0-0) = 0\,\textrm{.}

Hinweis: Zeichnen wir die Graphe von \displaystyle y=\cos 5x, sehen wir, dass die gesamte Fläche oberhalb der x-Achse genauso groß ist wie die gesamte Fläche unterhalb der x-Achse ist.