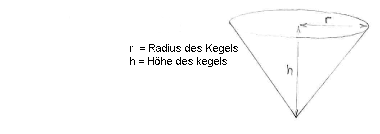Lösung 1.3:7

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Solution 1.3:7 moved to Lösung 1.3:7: Robot: moved page)
Aktuelle Version (18:10, 9. Sep. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 10 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
The whole procedure can be illustrated by the figure below:
+
Wie der Kegel gebaut wird, ist hier illustriert.
-
[[Image:1_3_7_1_1.gif|center]]
+
[[Image:1_3_7_1_1_de.gif|center]]
-
Because it is the cornet's volume we want to maximise, it is appropriate to start by introducing some notation for the dimensions of the cornet.
+
Da wir das Volumen des Kegels maximieren wollen, betrachten wir nun die Abmessungen Kegels.
-
[[Image:1_3_7_1_2.gif|center]]
+
[[Image:1_3_7_1_2_de.gif|center]]
-
With these dimensions, the volume of the cornet will be the same as that of a cone,
+
Mit diesen Abmessungen ist das Volumen des Kegels
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
-
V &= \frac{1}{3}\text{(area of upper circle)}\cdot\text{(height)}\\[5pt]
+
V &= \frac{1}{3}\text{(Fläche des Kreises)}\cdot\text{(Höhe)}\\[5pt]
&= \frac{1}{3}\pi r^{2}h\,\textrm{.}
&= \frac{1}{3}\pi r^{2}h\,\textrm{.}
\end{align}</math>}}
\end{align}</math>}}
-
To go further, we now need to express the radius <math>r</math> and the height <math>h</math> in terms of the angle <math>\alpha</math> on the removed circular sector, so that we can seek the maximum of the volume <math>V</math> when <math>\alpha </math> varies.
+
Wir müssen jetzt den Radius <math>r</math> und die Höhe <math>h</math> durch den Winkel <math>\alpha</math> ausdrücken, sodass wir das Volumen <math>V</math> als Funktion von <math>\alpha </math> schreiben können.
-
When we cut out a circular sector of angle <math>\alpha</math> from a circular disk, the remaining part of the circular disc's periphery will have length
+
Schneiden wir einen Kreissektor mit dem Winkel <math>\alpha</math> aus dem Kreis, ist der Umfang des übriggebliebenen Kreissegments
-
<math>(2\pi-\alpha)R</math>, where <math>R</math> is the radius of the circular disc. This periphery will then become the cornet's upper circular edge, which therefore has the same circumference.
+
<math>(2\pi-\alpha)R</math>, wobei <math>R</math> der ursprüngliche Radius ist.
-
[[Image:1_3_7_1_3.gif|center]]
+
[[Image:1_3_7_1_3_de.gif|center]]
-
On the other hand, the cornet's upper circular edge has a circumference
+
Der Umfang des oberen Kreises ist aber auch
-
<math>2\pi r</math>, so we must therefore have the relation
+
<math>2\pi r</math>, also haben wir
{{Abgesetzte Formel||<math>2\pi r = (2\pi-\alpha)R\quad\Leftrightarrow\quad r = \frac{2\pi -\alpha}{2\pi}\,R\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>2\pi r = (2\pi-\alpha)R\quad\Leftrightarrow\quad r = \frac{2\pi -\alpha}{2\pi}\,R\,\textrm{.}</math>}}
-
We have thus managed to express the radius <math>r</math> in terms of the angle
+
Jetzt haben wir den neuen Radius <math>r</math> als Funktion des Winkels
-
<math>\alpha</math> (and the radius <math>R</math> of the original circle).
+
<math>\alpha</math> und des ursprünglichen Radius <math>R</math> ausgedrückt.
-
In order to obtain the height <math>h</math>, we can use the fact that we know that the distance from the cornet's tip to its upper edge is equal to the radius <math>R</math> of the original circle. Pythagoras' theorem now gives
+
Um die Höhe zu bestimmen, benutzen wir den Satz des Pythagoras.
[[Image:1_3_7_1_4.gif||center]]
[[Image:1_3_7_1_4.gif||center]]
-
This means that
+
Also haben wir
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 41: Zeile 41:
\end{align}</math>}}
\end{align}</math>}}
-
Hence, we have expressed <math>r</math> and <math>h</math> in terms of the angle
+
Jetzt haben wir den Radius <math>r</math> und die Höhe <math>h</math> als Funktionen von
-
<math>\alpha</math> and the radius <math>R</math>, and we get that the volume of the cornet is given by
+
<math>\alpha</math> und <math>R</math> geschrieben. Das Volumen des Kegels ist also
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 50: Zeile 50:
\end{align}</math>}}
\end{align}</math>}}
-
At last, we can mathematically formulate the problem:
+
Unser Problem ist jetzt:
-
::Maximise <math>V(\alpha) = \frac{1}{3}\pi R^3 \Bigl(\frac{2\pi-\alpha}{2\pi} \Bigr)^2\sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,</math>, where <math>0\le \alpha \le 2\pi\,</math>.
+
::Maximiere <math>V(\alpha) = \frac{1}{3}\pi R^3 \Bigl(\frac{2\pi-\alpha}{2\pi} \Bigr)^2\sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,</math>, wo <math>0\le \alpha \le 2\pi\,</math>.
-
Before we start to try and solve this problem, we can observe that the variable
+
Bevor wir anfangen die Funktion abzuleiten, sehen wir, dass der Winkel
-
<math>\alpha</math> occurs in the volume function only in the combination
+
<math>\alpha</math> nur in
-
<math>(2\pi-\alpha)/2\pi</math>, so that we may as well choose to maximise the volume with respect to the variable <math>x=(2\pi-\alpha)/2\pi</math> to obtain, as far as the formula is concerned, the somewhat easier problem:
+
<math>(2\pi-\alpha)/2\pi</math>-Termen auftritt. Um das Problem zu vereinfachen, können wir das Volumen genauso in Bezug auf die Variable <math>x=(2\pi-\alpha)/2\pi</math> maximieren.
-
::Maximise <math>V(x) = \frac{1}{3}\pi R^3x^2\sqrt{1-x^2}\,</math>, when <math>0\le x\le 1\,</math>.
+
::Maximiere <math>V(x) = \frac{1}{3}\pi R^3x^2\sqrt{1-x^2}\ </math> , für <math>0\le x\le 1\,</math>.
-
When either <math>x=0</math> or <math>x=1</math>, the volume is zero and since the volume function is a differentiable function of <math>x</math> (apart from at <math>x=1</math>), the volume must be a maximum at a critical point of the function.
+
Wenn <math>x=0</math> oder <math>x=1</math> ist, ist das Volumen null. Weil die Funktion überall (außer in <math>x=1</math>) differenzierbar ist, nimmt das Volumen sein Maximum an einer stationären Stelle an.
-
We differentiate,
+
Wir leiten die Funktion ab
-
{{Abgesetzte Formel||<math>V'(x) = \frac{1}{3}\pi R^3\cdot 2x\cdot \sqrt{1-x^2} + \frac{1}{3}\pi R^3x^2\cdot\frac{1}{2\sqrt{1-x^2}}\cdot (-2x)\,,</math>}}
+
{{Abgesetzte Formel||<math>V'(x) = \frac{1}{3}\pi R^3\cdot 2x\cdot \sqrt{1-x^2} + \frac{1}{3}\pi R^3x^2\cdot\frac{1}{2\sqrt{1-x^2}}\cdot (-2x)\,</math>}}
-
and begin simplifying this expression. The strategy is to try to take out as many factors as possible, so that we see more easily when some factor, and hence the derivative, becomes zero,
+
und vereinfachen den Ausdruck, indem wir so viele Faktoren wir möglich herausziehen.
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
V'(x) &= \frac{2}{3}\pi R^3x\sqrt{1-x^2} - \frac{1}{3}\pi R^3x^3\frac{1}{\sqrt{1-x^2}}\\[5pt]
V'(x) &= \frac{2}{3}\pi R^3x\sqrt{1-x^2} - \frac{1}{3}\pi R^3x^3\frac{1}{\sqrt{1-x^2}}\\[5pt]
&= \frac{1}{3}\pi R^3\frac{x}{\sqrt{1-x^2}}\bigl[ 2(1-x^2)-x^2\bigr]\\[5pt]
&= \frac{1}{3}\pi R^3\frac{x}{\sqrt{1-x^2}}\bigl[ 2(1-x^2)-x^2\bigr]\\[5pt]
-
&= \frac{1}{3}\pi R^3\frac{x}{\sqrt{1-x^2}}(2-3x^2)\,\textrm{.}
+
&= \frac{1}{3}\pi R^3\frac{x}{\sqrt{1-x^2}}(2-3x^2)\,\textrm{}
\end{align}</math>}}
\end{align}</math>}}
-
The derivative is zero when <math>x=0</math> (which is an endpoint) or when <math>2-3x^2=0</math>, i.e. <math>x=\sqrt{2/3}\,</math>. (The point <math>x=-\sqrt{2/3}</math> lies outside <math>0\le x\le 1</math>.)
+
Die Ableitung ist null, wenn <math>x=0</math> (dies ist ein Randpunkt) oder wenn <math>2-3x^2=0</math> ist, also wenn <math>x=\sqrt{2/3}\,</math>. (Die Stelle <math>x=-\sqrt{2/3}</math> liegt außerhalb des Gebietes <math>0\le x\le 1</math>.)
-
 
+
-
With the help of a table of the sign of the factors,
+
 +
Durch eine Vorzeichentabelle erhalten wir die Vorzeichen der Faktoren
{| border="1" cellpadding="5" cellspacing="0" align="center"
{| border="1" cellpadding="5" cellspacing="0" align="center"
Zeile 111: Zeile 110:
-
we can write down a table of the sign of the derivative itself,
+
und erhalten dadurch das Vorzeichen der Ableitung selbst.
Zeile 138: Zeile 137:
|}
|}
 +
Wir sehen hier, dass die Funktion an der Stelle <math>x=\sqrt{2/3}</math> ein globales Maximum hat. <math>x = \sqrt{2/3}</math> entspricht dem Winkel <math>\alpha</math>:
-
and see that <math>x=\sqrt{2/3}</math> is a global maximum. The value <math>x = \sqrt{2/3}</math> corresponds to the <math>\alpha</math>-value
+
{{Abgesetzte Formel||<math>\sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\ </math>}}
-
 
+
-
{{Abgesetzte Formel||<math>\sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\ \text{radians.}</math>}}
+

Aktuelle Version

Wie der Kegel gebaut wird, ist hier illustriert.

Da wir das Volumen des Kegels maximieren wollen, betrachten wir nun die Abmessungen Kegels.

Mit diesen Abmessungen ist das Volumen des Kegels

\displaystyle \begin{align}

V &= \frac{1}{3}\text{(Fläche des Kreises)}\cdot\text{(Höhe)}\\[5pt] &= \frac{1}{3}\pi r^{2}h\,\textrm{.} \end{align}

Wir müssen jetzt den Radius \displaystyle r und die Höhe \displaystyle h durch den Winkel \displaystyle \alpha ausdrücken, sodass wir das Volumen \displaystyle V als Funktion von \displaystyle \alpha schreiben können.

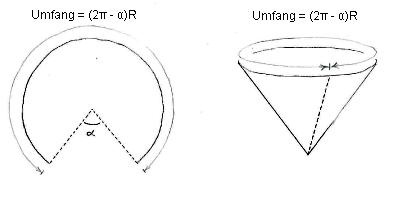
Schneiden wir einen Kreissektor mit dem Winkel \displaystyle \alpha aus dem Kreis, ist der Umfang des übriggebliebenen Kreissegments \displaystyle (2\pi-\alpha)R, wobei \displaystyle R der ursprüngliche Radius ist.

Der Umfang des oberen Kreises ist aber auch \displaystyle 2\pi r, also haben wir

\displaystyle 2\pi r = (2\pi-\alpha)R\quad\Leftrightarrow\quad r = \frac{2\pi -\alpha}{2\pi}\,R\,\textrm{.}

Jetzt haben wir den neuen Radius \displaystyle r als Funktion des Winkels \displaystyle \alpha und des ursprünglichen Radius \displaystyle R ausgedrückt.

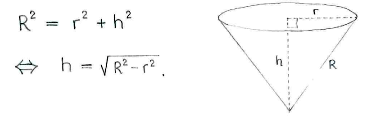
Um die Höhe zu bestimmen, benutzen wir den Satz des Pythagoras.

Also haben wir

\displaystyle \begin{align}

h &= \sqrt{R^2-\Bigl(\frac{2\pi-\alpha}{2\pi}\,R\Bigr)^2}\\[5pt] &= \sqrt{R^2-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2R^2}\\[5pt] &= R\sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,\textrm{.} \end{align}

Jetzt haben wir den Radius \displaystyle r und die Höhe \displaystyle h als Funktionen von \displaystyle \alpha und \displaystyle R geschrieben. Das Volumen des Kegels ist also

\displaystyle \begin{align}

V &= \frac{1}{3}\pi r^2 h\\[5pt] &= \frac{1}{3}\pi \Bigl(\frac{2\pi-\alpha}{2\pi}R\Bigr)^2 R\sqrt{1-\Bigl( \frac{2\pi-\alpha}{2\pi}\Bigr)^2}\\[5pt] &= \frac{1}{3}\pi R^3\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2 \sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,\textrm{.} \end{align}

Unser Problem ist jetzt:

Maximiere \displaystyle V(\alpha) = \frac{1}{3}\pi R^3 \Bigl(\frac{2\pi-\alpha}{2\pi} \Bigr)^2\sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,, wo \displaystyle 0\le \alpha \le 2\pi\,.

Bevor wir anfangen die Funktion abzuleiten, sehen wir, dass der Winkel \displaystyle \alpha nur in \displaystyle (2\pi-\alpha)/2\pi-Termen auftritt. Um das Problem zu vereinfachen, können wir das Volumen genauso in Bezug auf die Variable \displaystyle x=(2\pi-\alpha)/2\pi maximieren.

Maximiere \displaystyle V(x) = \frac{1}{3}\pi R^3x^2\sqrt{1-x^2}\ , für \displaystyle 0\le x\le 1\,.

Wenn \displaystyle x=0 oder \displaystyle x=1 ist, ist das Volumen null. Weil die Funktion überall (außer in \displaystyle x=1) differenzierbar ist, nimmt das Volumen sein Maximum an einer stationären Stelle an.

Wir leiten die Funktion ab

\displaystyle V'(x) = \frac{1}{3}\pi R^3\cdot 2x\cdot \sqrt{1-x^2} + \frac{1}{3}\pi R^3x^2\cdot\frac{1}{2\sqrt{1-x^2}}\cdot (-2x)\,

und vereinfachen den Ausdruck, indem wir so viele Faktoren wir möglich herausziehen.

\displaystyle \begin{align}

V'(x) &= \frac{2}{3}\pi R^3x\sqrt{1-x^2} - \frac{1}{3}\pi R^3x^3\frac{1}{\sqrt{1-x^2}}\\[5pt] &= \frac{1}{3}\pi R^3\frac{x}{\sqrt{1-x^2}}\bigl[ 2(1-x^2)-x^2\bigr]\\[5pt] &= \frac{1}{3}\pi R^3\frac{x}{\sqrt{1-x^2}}(2-3x^2)\,\textrm{} \end{align}

Die Ableitung ist null, wenn \displaystyle x=0 (dies ist ein Randpunkt) oder wenn \displaystyle 2-3x^2=0 ist, also wenn \displaystyle x=\sqrt{2/3}\,. (Die Stelle \displaystyle x=-\sqrt{2/3} liegt außerhalb des Gebietes \displaystyle 0\le x\le 1.)

Durch eine Vorzeichentabelle erhalten wir die Vorzeichen der Faktoren

\displaystyle x \displaystyle 0 \displaystyle \sqrt{\tfrac{2}{3}} \displaystyle 1
\displaystyle x \displaystyle 0 \displaystyle + \displaystyle + \displaystyle + \displaystyle +
\displaystyle \sqrt{1-x^2} \displaystyle + \displaystyle + \displaystyle + \displaystyle + \displaystyle 0
\displaystyle 2-3x^2 \displaystyle + \displaystyle + \displaystyle 0 \displaystyle - \displaystyle -


und erhalten dadurch das Vorzeichen der Ableitung selbst.


\displaystyle x \displaystyle 0 \displaystyle \sqrt{\tfrac{2}{3}} \displaystyle 1
\displaystyle V'(x) \displaystyle 0 \displaystyle + \displaystyle 0 \displaystyle -  
\displaystyle V(x) \displaystyle 0 \displaystyle \nearrow \displaystyle \tfrac{4}{9\sqrt{3}}\pi R^3 \displaystyle \searrow \displaystyle 0

Wir sehen hier, dass die Funktion an der Stelle \displaystyle x=\sqrt{2/3} ein globales Maximum hat. \displaystyle x = \sqrt{2/3} entspricht dem Winkel \displaystyle \alpha:

\displaystyle \sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:7“