Lösung 1.3:2c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Aktuelle Version (17:42, 9. Sep. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 6 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
There are three types of points at which the function can have local extreme points,
+
Lokale Extremstellen einer Funktion sind entweder:
-
# critical points, i.e. where <math>f^{\,\prime}(x)=0</math>,
+
# stationäre Stellen mit <math>f^{\,\prime}(x)=0</math>,
-
# points where the function is not differentiable, and
+
# singuläre Stellen, in denen die Funktion nicht differenzierbar ist, oder
-
# endpoints of the interval of definition.
+
# Randstellen.
 +
 +
Da die Funktion ein Polynom ist, ist sie überall definiert und überall differenzierbar. Also gibt es keine Extremstellen, die die Bedingungen 2 und 3 erfüllen.
-
Because our function is a polynomial, it is defined and differentiable everywhere, and therefore does not have any points which satisfy items 2 and 3.
+
Die Ableitung null gesetzt, ergibt folgende Gleichung
-
 
+
-
As regards item 1, we set the derivative equal to zero and obtain the equation
+
{{Abgesetzte Formel||<math>f^{\,\prime}(x) = 6x^2+6x-12 = 0\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>f^{\,\prime}(x) = 6x^2+6x-12 = 0\,\textrm{.}</math>}}
-
Dividing both sides by 6 and completing the square, we obtain
+
Dividieren wir durch 6 erhalten wir durch quadratische Ergänzung
{{Abgesetzte Formel||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 - 2 = 0\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 - 2 = 0\,\textrm{.}</math>}}
-
This gives us the equation
+
Und wir erhalten die Gleichung
{{Abgesetzte Formel||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 = \frac{9}{4}</math>}}
{{Abgesetzte Formel||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 = \frac{9}{4}</math>}}
-
and taking the square root gives the solutions
+
mit den Lösungen
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 26: Zeile 26:
\end{align}</math>}}
\end{align}</math>}}
-
This means that if the function has several extreme points, they must be among
+
Die Funktion hat also die stationären Stellen <math>x=-2</math> und <math>x=1</math>.
-
<math>x=-2</math> and <math>x=1</math>.
+
-
Then, we write down a sign table for the derivative, and read off the possible extreme points.
+
Wir erstellen eine Vorzeichentabelle und erhalten so die Extremstellen.
{| border="1" cellpadding="5" cellspacing="0" align="center"
{| border="1" cellpadding="5" cellspacing="0" align="center"
Zeile 55: Zeile 54:
|}
|}
 +
Die Funktion hat also ein lokales Maximum an der Stelle <math>x=-2</math> und ein lokales Minimum an der Stelle <math>x=1</math>.
-
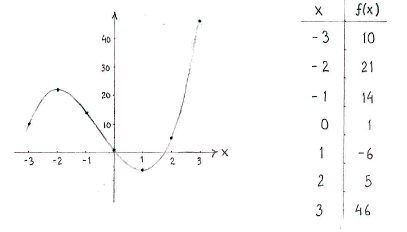
The function has a local maximum at <math>x=-2</math> and a local minimum at <math>x=1</math>.
+
Berechnen wir die Funktionswerte von einigen Stellen, können wir mit Hilfe der Vorzeichentabelle die Funktion zeichnen.
-
 
+
-
We obtain the overall appearance of the graph of the function from the table and by calculating the value of the function at a few points.
+
[[Image:1_3_2_c.gif|center]]
[[Image:1_3_2_c.gif|center]]

Aktuelle Version

Lokale Extremstellen einer Funktion sind entweder:

  1. stationäre Stellen mit \displaystyle f^{\,\prime}(x)=0,
  2. singuläre Stellen, in denen die Funktion nicht differenzierbar ist, oder
  3. Randstellen.

Da die Funktion ein Polynom ist, ist sie überall definiert und überall differenzierbar. Also gibt es keine Extremstellen, die die Bedingungen 2 und 3 erfüllen.

Die Ableitung null gesetzt, ergibt folgende Gleichung

\displaystyle f^{\,\prime}(x) = 6x^2+6x-12 = 0\,\textrm{.}

Dividieren wir durch 6 erhalten wir durch quadratische Ergänzung

\displaystyle \Bigl(x+\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 - 2 = 0\,\textrm{.}

Und wir erhalten die Gleichung

\displaystyle \Bigl(x+\frac{1}{2}\Bigr)^2 = \frac{9}{4}

mit den Lösungen

\displaystyle \begin{align}

x &= -\frac{1}{2}-\sqrt{\frac{9}{4}} = -\frac{1}{2}-\frac{3}{2} = -2\,,\\[5pt] x &= -\frac{1}{2}+\sqrt{\frac{9}{4}} = -\frac{1}{2}+\frac{3}{2} = 1\,\textrm{.} \end{align}

Die Funktion hat also die stationären Stellen \displaystyle x=-2 und \displaystyle x=1.

Wir erstellen eine Vorzeichentabelle und erhalten so die Extremstellen.

\displaystyle x \displaystyle -2 \displaystyle 1
\displaystyle f^{\,\prime}(x) \displaystyle + \displaystyle 0 \displaystyle - \displaystyle 0 \displaystyle +
\displaystyle f(x) \displaystyle \nearrow \displaystyle 21 \displaystyle \searrow \displaystyle -6 \displaystyle \nearrow

Die Funktion hat also ein lokales Maximum an der Stelle \displaystyle x=-2 und ein lokales Minimum an der Stelle \displaystyle x=1.

Berechnen wir die Funktionswerte von einigen Stellen, können wir mit Hilfe der Vorzeichentabelle die Funktion zeichnen.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:2c“