Lösung 3.3:6

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Aktuelle Version (12:52, 3. Sep. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 6 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
We take up the exercise's challenge and solve the equation both in polar form and in the form <math>a+ib</math>.
+
'''Polarform'''
 +
Wir schreiben die Gleichung zuerst in Polarform
-
'''Polar form'''
+
{{Abgesetzte Formel||<math>\begin{align}
-
 
+
-
In polar form,
+
-
 
+
-
{{Displayed math||<math>\begin{align}
+
z &= r\,(\cos\alpha + i\sin\alpha)\,,\\[5pt]
z &= r\,(\cos\alpha + i\sin\alpha)\,,\\[5pt]
-
1+i &= \sqrt{2}\Bigl(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,,
+
1+i &= \sqrt{2}\Bigl(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,
\end{align}</math>}}
\end{align}</math>}}
-
and, using de Moivre's formula, the equation becomes
+
und durch den Moivrischen Satz erhalten wir die Gleichung
-
{{Displayed math||<math>r^2(\cos 2\alpha + i\sin 2\alpha) = \sqrt{2}\Bigl(\cos \frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>r^2(\cos 2\alpha + i\sin 2\alpha) = \sqrt{2}\Bigl(\cos \frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,\textrm{.}</math>}}
-
If both sides are to be equal, their magnitudes must be equal and their arguments must be equal, other than for multiples of <math>2\pi</math>,
+
Damit die beiden Seiten gleich sind, müssen die Beträge der beiden Seiten gleich sein und die Argumente der beiden Seiten dürfen sich nur um ein Vielfaches von <math>2\pi</math> unterscheiden
-
{{Displayed math||<math>\left\{\begin{align}
+
{{Abgesetzte Formel||<math>\left\{\begin{align}
r^2 &= \sqrt{2}\,,\\[5pt]
r^2 &= \sqrt{2}\,,\\[5pt]
-
2\alpha &= \frac{\pi}{4}+2n\pi\,,\quad\text{(n is an arbitrary integer).}
+
2\alpha &= \frac{\pi}{4}+2n\pi\,.\quad
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
This gives
+
Das ergibt
-
{{Displayed math||<math>\left\{\begin{align}
+
{{Abgesetzte Formel||<math>\left\{\begin{align}
r &= \sqrt{\sqrt{2}} = \bigl(2^{1/2}\bigr)^{1/2} = 2^{1/4} = \sqrt[4]{2}\,,\\[5pt]
r &= \sqrt{\sqrt{2}} = \bigl(2^{1/2}\bigr)^{1/2} = 2^{1/4} = \sqrt[4]{2}\,,\\[5pt]
-
\alpha &= \frac{\pi}{8}+n\pi\,,\quad\text{(n is an arbitrary integer),}
+
\alpha &= \frac{\pi}{8}+n\pi\,.\quad
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
which corresponds two solutions, because all even values of <math>n</math> give the argument <math>\pi/8</math>, to within multiples of <math>2\pi</math>, and all odd values of <math>n</math> give the argument <math>9\pi/8</math>, to within a multiple of <math>2\pi</math>.
+
Das entspricht zwei Lösungen, da alle geraden Zahlen dem Argument <math>\pi/8</math> entsprechen, plus ein Vielfaches von <math>2\pi</math> und alle ungerade Zahlen dem Argument <math>9\pi/8</math> entsprechen, plus ein Vielfaches von <math>2\pi</math>.
-
Thus, in polar form, we have the solutions,
+
In Polarform lauten die Lösungen also
-
{{Displayed math||<math>z = \left\{\begin{align}
+
{{Abgesetzte Formel||<math>z = \left\{\begin{align}
&\sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8}\Bigr)\,,\\[5pt]
&\sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8}\Bigr)\,,\\[5pt]
&\sqrt[4]{2}\Bigl(\cos\frac{9\pi}{8} + i\sin\frac{9\pi}{8}\Bigr)\,\textrm{.}
&\sqrt[4]{2}\Bigl(\cos\frac{9\pi}{8} + i\sin\frac{9\pi}{8}\Bigr)\,\textrm{.}
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
One solution <math>z=\sqrt[4]{2}(\cos (\pi/8) + i\sin (\pi/8)</math> lies in the first quadrant and the second solution <math>z=\sqrt[4]{2}(\cos (9\pi/8) + i\sin (9\pi/8))</math> lies in the third quadrant.
+
 
 +
Eine Lösung, <math>z=\sqrt[4]{2}(\cos (\pi/8) + i\sin (\pi/8)</math>, liegt im ersten Quadrant und die zweite Lösung, <math>z=\sqrt[4]{2}(\cos (9\pi/8) + i\sin (9\pi/8))</math>, liegt im dritten Quadrant.
[[Image:3_3_6.gif|center]]
[[Image:3_3_6.gif|center]]
-
'''Rectangular form'''
+
''' In der Form ''a'' + ''bi'' '''
-
The alternative way to solve the equation is to put <math>z=x+iy</math> and to try to solve the equation for <math>x</math> and <math>y</math>.
+
Wir schreiben hier <math>z=x+iy</math> und versuchen die Konstanten <math>x</math> und <math>y</math> zu bestimmen.
-
If <math>z=x+iy</math>, the equation becomes
+
Mit <math>z=x+iy</math> erhalten wir die Gleichung
-
{{Displayed math||<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
(x+iy)^2 &= 1+i\,,\\[5pt]
(x+iy)^2 &= 1+i\,,\\[5pt]
x^2-y^2+2xyi &= 1+i\,\textrm{.}
x^2-y^2+2xyi &= 1+i\,\textrm{.}
\end{align}</math>}}
\end{align}</math>}}
-
Because both sides' real and imaginary parts must equal each other we have that
+
Da der Real- und Imaginärteil der beiden Seiten gleich sein muss, erhalten wir
-
{{Displayed math||<math>\left\{\begin{align}
+
{{Abgesetzte Formel||<math>\left\{\begin{align}
x^2 - y^2 &= 1\,,\\[5pt]
x^2 - y^2 &= 1\,,\\[5pt]
2xy &= 1\,\textrm{.}
2xy &= 1\,\textrm{.}
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
All the information we need for determining <math>x</math> and <math>y</math> is in these two equations, but it will make things easier if we include an extra relation: the magnitude of both sides should be equal,
+
Wir können hier <math>x</math> und <math>y</math> direkt bestimmen, aber um es einfacher zu machen, berechnen wir den Betrag von beiden Seiten
-
{{Displayed math||<math>x^2 + y^2 = \sqrt{1^2+1^2} = \sqrt{2}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>x^2 + y^2 = \sqrt{1^2+1^2} = \sqrt{2}\,\textrm{.}</math>}}
-
Therefore, we have in total three equations,
+
Wir erhalten insgesamt drei Gleichungen
-
{{Displayed math||<math>\left\{\begin{align}
+
{{Abgesetzte Formel||<math>\left\{\begin{align}
x^2 -y^2 &= 1\,,\\[5pt]
x^2 -y^2 &= 1\,,\\[5pt]
2xy &= 1\,,\\[5pt]
2xy &= 1\,,\\[5pt]
Zeile 73: Zeile 71:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
If we add the first and the third equations,
+
Addieren wir die erste Gleichung zur dritten erhalten wir
{| align="center" style="padding:10px 0px 10px 0px;"
{| align="center" style="padding:10px 0px 10px 0px;"
||
||
Zeile 99: Zeile 97:
|}
|}
-
we get that <math>x</math> must be equal to
+
und wir erhalten
-
{{Displayed math||<math>x=\pm \sqrt{\frac{\sqrt{2}+1}{2}}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>x=\pm \sqrt{\frac{\sqrt{2}+1}{2}}\,\textrm{.}</math>}}
-
If we subtract the first equation from the third equation,
+
Subtrahieren wir die erste Gleichung von der dritten, erhalten wir
{| align="center" style="padding:10px 0px 10px 0px;"
{| align="center" style="padding:10px 0px 10px 0px;"
||
||
Zeile 129: Zeile 127:
|}
|}
-
we obtain that <math>y</math> must be equal to
+
und das ergibt
-
{{Displayed math||<math>y=\pm \sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>y=\pm \sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}</math>}}
-
All in all, this gives us four possible solutions
+
Insgesamt haben wir also vier mögliche Lösungen.
-
{{Displayed math||<math>\left\{\begin{align}
+
{{Abgesetzte Formel||<math>\left\{\begin{align}
x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt]
x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt]
y &= \sqrt{\frac{\sqrt{2}-1}{2}}
y &= \sqrt{\frac{\sqrt{2}-1}{2}}
Zeile 155: Zeile 153:
\end{align} \right.</math>}}
\end{align} \right.</math>}}
-
although we have only taken account of the first and third equations.
+
Die zweite Gleichung sagt auch, dass <math>xy</math> positiv sein soll. Wir behalten daher nur die Gleichungen.
-
 
+
-
The second equation says that the product <math>xy</math> should be positive and then we can directly get rid of solutions in which <math>x</math> and <math>y</math>
+
-
have different signs. Thus, all that is left is
+
-
{{Displayed math||<math>\left\{\begin{align}
+
{{Abgesetzte Formel||<math>\left\{\begin{align}
x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt]
x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt]
y &= \sqrt{\frac{\sqrt{2}-1}{2}}
y &= \sqrt{\frac{\sqrt{2}-1}{2}}
\end{align}\right.
\end{align}\right.
-
\qquad\text{and}\qquad
+
\qquad\text{und}\qquad
\left\{\begin{align}
\left\{\begin{align}
x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt]
x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt]
Zeile 170: Zeile 165:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
Now, we know already that the equation has two solutions, so we can draw the conclusion that these are
+
Nachdem wir wissen, dass unsere Gleichung zwei Lösungen hat, müssen diese unsere Lösungen sein
-
{{Displayed math||<math>z = \left\{\begin{align}
+
{{Abgesetzte Formel||<math>z = \left\{\begin{align}
\sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}\,,\\[5pt]
\sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}\,,\\[5pt]
-\sqrt{\frac{\sqrt{2}+1}{2}} - i\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}
-\sqrt{\frac{\sqrt{2}+1}{2}} - i\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
If we compare the solution in the first quadrant when it is expressed in polar and rectangular forms, we have
+
Vergleichen wir diese Lösungen mit den Lösungen in Polarform, erhalten wir
-
{{Displayed math||<math>\sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8} \Bigr) = \sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}</math>}}
+
{{Abgesetzte Formel||<math>\sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8} \Bigr) = \sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}</math>}}
-
and therefore we must have that
+
und daraus folgt
-
{{Displayed math||<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
\cos\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}+1}{2}}\,,\\[5pt]
\cos\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}+1}{2}}\,,\\[5pt]
\sin\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}
\sin\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}
\end{align}</math>}}
\end{align}</math>}}
-
Thus, we have
+
Wir erhalten auch
-
{{Displayed math||<math>\tan\frac{\pi}{8} = \frac{\sin\dfrac{\pi}{8}}{\cos\dfrac{\pi}{8}} = \frac{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}-1}{2}}}{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}+1}{2}}} = \sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>\tan\frac{\pi}{8} = \frac{\sin\dfrac{\pi}{8}}{\cos\dfrac{\pi}{8}} = \frac{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}-1}{2}}}{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}+1}{2}}} = \sqrt {\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\,\textrm{.}</math>}}
-
We can simplify the expression under the square root sign by multiplying top and bottom by the conjugate of the denominator,
+
Wir können diesen Ausdruck vereinfachen, indem wir den Ausdruck mit dem konjugierten Nenner erweitern
-
{{Displayed math||<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
\tan\frac{\pi}{8}
\tan\frac{\pi}{8}
-
&= \sqrt{\frac{(\sqrt{2}-1)(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}}
+
&= \sqrt {\frac{(\sqrt{2}-1)(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}}
-
= \sqrt{\frac{(\sqrt{2}-1)^2}{(\sqrt{2})^2-1^2}}\\[5pt]
+
= \sqrt {\frac{(\sqrt{2}-1)^2}{(\sqrt{2})^2-1^2}}\\[5pt]
&= \sqrt{\frac{(\sqrt{2}-1)^2}{2-1}}
&= \sqrt{\frac{(\sqrt{2}-1)^2}{2-1}}
= \sqrt{(\sqrt{2}-1)^2}
= \sqrt{(\sqrt{2}-1)^2}
= \sqrt{2}-1\,\textrm{.}
= \sqrt{2}-1\,\textrm{.}
\end{align}</math>}}
\end{align}</math>}}

Aktuelle Version

Polarform

Wir schreiben die Gleichung zuerst in Polarform

\displaystyle \begin{align}

z &= r\,(\cos\alpha + i\sin\alpha)\,,\\[5pt] 1+i &= \sqrt{2}\Bigl(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\, \end{align}

und durch den Moivrischen Satz erhalten wir die Gleichung

\displaystyle r^2(\cos 2\alpha + i\sin 2\alpha) = \sqrt{2}\Bigl(\cos \frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,\textrm{.}

Damit die beiden Seiten gleich sind, müssen die Beträge der beiden Seiten gleich sein und die Argumente der beiden Seiten dürfen sich nur um ein Vielfaches von \displaystyle 2\pi unterscheiden

\displaystyle \left\{\begin{align}

r^2 &= \sqrt{2}\,,\\[5pt] 2\alpha &= \frac{\pi}{4}+2n\pi\,.\quad \end{align}\right.

Das ergibt

\displaystyle \left\{\begin{align}

r &= \sqrt{\sqrt{2}} = \bigl(2^{1/2}\bigr)^{1/2} = 2^{1/4} = \sqrt[4]{2}\,,\\[5pt] \alpha &= \frac{\pi}{8}+n\pi\,.\quad \end{align}\right.

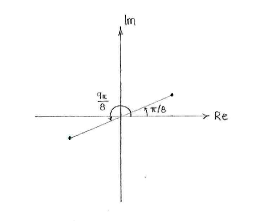
Das entspricht zwei Lösungen, da alle geraden Zahlen dem Argument \displaystyle \pi/8 entsprechen, plus ein Vielfaches von \displaystyle 2\pi und alle ungerade Zahlen dem Argument \displaystyle 9\pi/8 entsprechen, plus ein Vielfaches von \displaystyle 2\pi.

In Polarform lauten die Lösungen also

\displaystyle z = \left\{\begin{align}

&\sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8}\Bigr)\,,\\[5pt] &\sqrt[4]{2}\Bigl(\cos\frac{9\pi}{8} + i\sin\frac{9\pi}{8}\Bigr)\,\textrm{.} \end{align}\right.


Eine Lösung, \displaystyle z=\sqrt[4]{2}(\cos (\pi/8) + i\sin (\pi/8), liegt im ersten Quadrant und die zweite Lösung, \displaystyle z=\sqrt[4]{2}(\cos (9\pi/8) + i\sin (9\pi/8)), liegt im dritten Quadrant.


In der Form a + bi

Wir schreiben hier \displaystyle z=x+iy und versuchen die Konstanten \displaystyle x und \displaystyle y zu bestimmen.

Mit \displaystyle z=x+iy erhalten wir die Gleichung

\displaystyle \begin{align}

(x+iy)^2 &= 1+i\,,\\[5pt] x^2-y^2+2xyi &= 1+i\,\textrm{.} \end{align}

Da der Real- und Imaginärteil der beiden Seiten gleich sein muss, erhalten wir

\displaystyle \left\{\begin{align}

x^2 - y^2 &= 1\,,\\[5pt] 2xy &= 1\,\textrm{.} \end{align}\right.

Wir können hier \displaystyle x und \displaystyle y direkt bestimmen, aber um es einfacher zu machen, berechnen wir den Betrag von beiden Seiten

\displaystyle x^2 + y^2 = \sqrt{1^2+1^2} = \sqrt{2}\,\textrm{.}

Wir erhalten insgesamt drei Gleichungen

\displaystyle \left\{\begin{align}

x^2 -y^2 &= 1\,,\\[5pt] 2xy &= 1\,,\\[5pt] x^2 + y^2 &= \sqrt{2}\,\textrm{.} \end{align}\right.

Addieren wir die erste Gleichung zur dritten erhalten wir

\displaystyle x^2 \displaystyle {}-{} \displaystyle y^2 \displaystyle {}={} \displaystyle 1
\displaystyle +\ \ \displaystyle x^2 \displaystyle {}+{} \displaystyle y^2 \displaystyle {}={} \displaystyle \sqrt{2}
\displaystyle 2x^2 \displaystyle {}={} \displaystyle \sqrt{2}+1

und wir erhalten

\displaystyle x=\pm \sqrt{\frac{\sqrt{2}+1}{2}}\,\textrm{.}

Subtrahieren wir die erste Gleichung von der dritten, erhalten wir

\displaystyle x^2 \displaystyle {}+{} \displaystyle y^2 \displaystyle {}={} \displaystyle \sqrt{2}
\displaystyle -\ \ \displaystyle \bigl(x^2 \displaystyle {}-{} \displaystyle y^2 \displaystyle {}={} \displaystyle 1\bigr)
\displaystyle 2y^2 \displaystyle {}={} \displaystyle \sqrt{2}-1

und das ergibt

\displaystyle y=\pm \sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}

Insgesamt haben wir also vier mögliche Lösungen.

\displaystyle \left\{\begin{align}

x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align} \right.

Die zweite Gleichung sagt auch, dass \displaystyle xy positiv sein soll. Wir behalten daher nur die Gleichungen.

\displaystyle \left\{\begin{align}

x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \qquad\text{und}\qquad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right.

Nachdem wir wissen, dass unsere Gleichung zwei Lösungen hat, müssen diese unsere Lösungen sein

\displaystyle z = \left\{\begin{align}

\sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}\,,\\[5pt] -\sqrt{\frac{\sqrt{2}+1}{2}} - i\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.} \end{align}\right.

Vergleichen wir diese Lösungen mit den Lösungen in Polarform, erhalten wir

\displaystyle \sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8} \Bigr) = \sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}

und daraus folgt

\displaystyle \begin{align}

\cos\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}+1}{2}}\,,\\[5pt] \sin\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.} \end{align}

Wir erhalten auch

\displaystyle \tan\frac{\pi}{8} = \frac{\sin\dfrac{\pi}{8}}{\cos\dfrac{\pi}{8}} = \frac{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}-1}{2}}}{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}+1}{2}}} = \sqrt {\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\,\textrm{.}

Wir können diesen Ausdruck vereinfachen, indem wir den Ausdruck mit dem konjugierten Nenner erweitern

\displaystyle \begin{align}

\tan\frac{\pi}{8} &= \sqrt {\frac{(\sqrt{2}-1)(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}} = \sqrt {\frac{(\sqrt{2}-1)^2}{(\sqrt{2})^2-1^2}}\\[5pt] &= \sqrt{\frac{(\sqrt{2}-1)^2}{2-1}} = \sqrt{(\sqrt{2}-1)^2} = \sqrt{2}-1\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.3:6“