Lösung 3.2:6f

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Aktuelle Version (17:19, 22. Aug. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 3 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
We can write every factor in the numerator and denominator in polar form and then use the arithmetical rules for multiplication and division in polar form:
+
Schreiben wir den Zähler und Nenner in Polarform, können wir die Divisions- und Multilpikationsregeln für komplexe Zahlen in Polarform verwenden:
:*<math>r_1(\cos\alpha + i\sin\alpha)\cdot r_2(\cos\beta + i\sin\beta) = r_1r_2\bigl(\cos(\alpha+\beta)+i\sin(\alpha+\beta)\bigr)\,,</math>
:*<math>r_1(\cos\alpha + i\sin\alpha)\cdot r_2(\cos\beta + i\sin\beta) = r_1r_2\bigl(\cos(\alpha+\beta)+i\sin(\alpha+\beta)\bigr)\,,</math>
Zeile 5: Zeile 5:
:*<math>\frac{r_1(\cos\alpha + i\sin\alpha)}{r_2(\cos\beta + i\sin\beta)} = \frac{r_1}{r_2}\bigl(\cos(\alpha-\beta) + i\sin (\alpha-\beta)\bigr)\,\textrm{.}</math>
:*<math>\frac{r_1(\cos\alpha + i\sin\alpha)}{r_2(\cos\beta + i\sin\beta)} = \frac{r_1}{r_2}\bigl(\cos(\alpha-\beta) + i\sin (\alpha-\beta)\bigr)\,\textrm{.}</math>
-
In fact, most of the work consists of writing all the factors in polar form:
+
Wir schreiben die Zahlen also in Polarform:
{| align="center"
{| align="center"
Zeile 15: Zeile 15:
|}
|}
-
The whole expression becomes
+
und erhalten den Ausdruck
-
{{Displayed math||<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
\frac{(2+2i)(1+i\sqrt{3}\,)}{3i(\sqrt{12}-2i)}
\frac{(2+2i)(1+i\sqrt{3}\,)}{3i(\sqrt{12}-2i)}
&= \frac{2\sqrt{2}\Bigl(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}\Bigr)\cdot 2\Bigl( \cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}\Bigr)}{3\Bigl(\cos\dfrac{\pi}{2}+i\sin \dfrac{\pi}{2}\Bigr)\cdot 4\Bigl(\cos\Bigl(-\dfrac{\pi}{6}\Bigr)+i\sin\Bigl(-\dfrac{\pi}{6}\Bigr)\Bigr)}\\[5pt]
&= \frac{2\sqrt{2}\Bigl(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}\Bigr)\cdot 2\Bigl( \cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}\Bigr)}{3\Bigl(\cos\dfrac{\pi}{2}+i\sin \dfrac{\pi}{2}\Bigr)\cdot 4\Bigl(\cos\Bigl(-\dfrac{\pi}{6}\Bigr)+i\sin\Bigl(-\dfrac{\pi}{6}\Bigr)\Bigr)}\\[5pt]

Aktuelle Version

Schreiben wir den Zähler und Nenner in Polarform, können wir die Divisions- und Multilpikationsregeln für komplexe Zahlen in Polarform verwenden:

  • \displaystyle r_1(\cos\alpha + i\sin\alpha)\cdot r_2(\cos\beta + i\sin\beta) = r_1r_2\bigl(\cos(\alpha+\beta)+i\sin(\alpha+\beta)\bigr)\,,
  • \displaystyle \frac{r_1(\cos\alpha + i\sin\alpha)}{r_2(\cos\beta + i\sin\beta)} = \frac{r_1}{r_2}\bigl(\cos(\alpha-\beta) + i\sin (\alpha-\beta)\bigr)\,\textrm{.}

Wir schreiben die Zahlen also in Polarform:

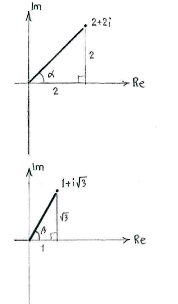
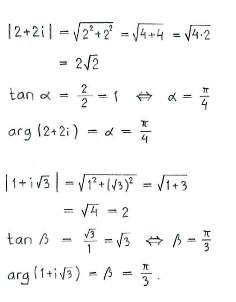
Image:3_2_6_f1_bild.gif Image:3_2_6_f1_bildtext.gif
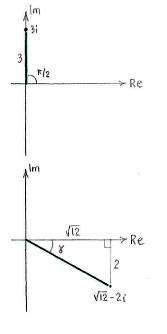
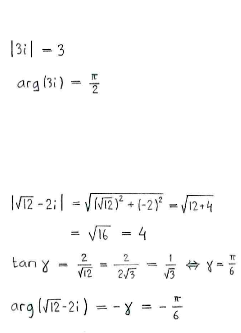
Image:3_2_6_f2_bild.gif Image:3_2_6_f2_bildtext.gif

und erhalten den Ausdruck

\displaystyle \begin{align}

\frac{(2+2i)(1+i\sqrt{3}\,)}{3i(\sqrt{12}-2i)} &= \frac{2\sqrt{2}\Bigl(\cos\dfrac{\pi}{4}+i\sin\dfrac{\pi}{4}\Bigr)\cdot 2\Bigl( \cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}\Bigr)}{3\Bigl(\cos\dfrac{\pi}{2}+i\sin \dfrac{\pi}{2}\Bigr)\cdot 4\Bigl(\cos\Bigl(-\dfrac{\pi}{6}\Bigr)+i\sin\Bigl(-\dfrac{\pi}{6}\Bigr)\Bigr)}\\[5pt] &= \frac{4\sqrt{2}\Bigl(\cos\Bigl(\dfrac{\pi}{4}+\dfrac{\pi}{3}\Bigr) + i\sin\Bigl( \dfrac{\pi}{4}+\dfrac{\pi}{3}\Bigr)\Bigr)}{12\Bigl(\cos\Bigl(\dfrac{\pi}{2}-\dfrac{\pi}{6}\Bigr)+i\sin\Bigl(\dfrac{\pi}{2}-\dfrac{\pi}{6}\Bigr)\Bigr)}\\[5pt] &= \frac{4\sqrt{2}\Bigl(\cos\dfrac{7\pi}{12}+i\sin\dfrac{7\pi}{12}\Bigr)}{12\Bigl(\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}\Bigr)}\\[5pt] &= \frac{4\sqrt{2}}{12}\Bigl(\cos\Bigl(\frac{7\pi}{12}-\frac{\pi}{3}\Bigr) + i\sin \Bigl(\frac{7\pi}{12}-\frac{\pi}{3}\Bigr)\Bigr)\\[5pt] &= \frac{\sqrt{2}}{3}\Bigl(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:6f“