Lösung 3.3:1c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Aktuelle Version (07:48, 1. Sep. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 5 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
The calculation follows a fairly set pattern. We write the number
+
Wir bringen zuerst <math>4\sqrt{3}-4i</math> in Polarform und verwenden dann den Moivreschen Satz.
-
<math>4\sqrt{3}-4i</math>
+
-
in polar form and then use de Moivre's formula.
+
 +
<center>[[Image:3_3_1_c.gif]] [[Image:3_3_1_c_text.gif]]</center>
-
[[Image:3_3_1_c.gif]] [[Image:3_3_1_c_text.gif]]
+
Dies ergibt
 +
{{Abgesetzte Formel||<math>4\sqrt{3}-4i = 8\Bigl(\cos\Bigl(-\frac{\pi}{6}\Bigr) + i\sin\Bigl(-\frac{\pi}{6}\Bigr)\Bigr)</math>}}
-
This gives
+
und durch den Moivreschen Satz erhalten wir
-
 
+
{{Abgesetzte Formel||<math>\begin{align}
-
<math>4\sqrt{3}-4i=8\left( \cos \left( -\frac{\pi }{6} \right)+i\sin \left( -\frac{\pi }{6} \right) \right)</math>
+
\bigl(4\sqrt{3}-4i\bigr)^{22}
-
 
+
&= 8^{22}\Bigl(\cos\Bigl(22\cdot\Bigl(-\frac{\pi}{6}\Bigr)\Bigr) + i\sin\Bigl(22\cdot\Bigl(-\frac{\pi}{6}\Bigr)\Bigr)\Bigr)\\[5pt]
-
 
+
&= \bigl(2^3\bigr)^{22}\Bigl(\cos\Bigl(-\frac{11\pi}{3}\Bigr) + i\sin\Bigl(-\frac{11\pi}{3}\Bigr)\Bigr)\\[5pt]
-
and then we get, on using de Moivre's formula,
+
&= 2^{3\cdot 22}\Bigl(\cos\Bigl(-\frac{12\pi -\pi }{3}\Bigr) + i\sin\Bigl(-\frac{12\pi -\pi}{3}\Bigr)\Bigr)\\[5pt]
-
 
+
&= 2^{66}\Bigl(\cos\Bigl(-4\pi+\frac{\pi}{3}\Bigr) + i\sin\Bigl(-4\pi+\frac{\pi}{3} \Bigr)\Bigr)\\[5pt]
-
 
+
&= 2^{66}\Bigl(\cos\frac{\pi}{3} + i\sin\frac{\pi}{3}\Bigr)\\[5pt]
-
<math>\begin{align}
+
&= 2^{66}\Bigl(\frac{1}{2} + i\frac{\sqrt{3}}{2}\Bigr)\\[5pt]
-
& \left( 4\sqrt{3}-4i \right)^{22}=8^{22}\left( \cos \left( 22\centerdot \left( -\frac{\pi }{6} \right) \right)+i\sin \left( 22\centerdot \left( -\frac{\pi }{6} \right) \right) \right) \\
+
&= 2^{65}(1+i\sqrt{3}\,)\,\textrm{.}
-
& =\left( 2^{3} \right)^{22}\left( \cos \left( -\frac{11\pi }{3} \right)+i\sin \left( -\frac{11\pi }{3} \right) \right) \\
+
\end{align}</math>}}
-
& =2^{3\centerdot 22}\left( \cos \left( -\frac{12\pi -\pi }{3} \right)+i\sin \left( -\frac{12\pi -\pi }{3} \right) \right) \\
+
-
& =2^{66}\left( \cos \left( -4\pi +\frac{\pi }{3} \right)+i\sin \left( -4\pi +\frac{\pi }{3} \right) \right) \\
+
-
& =2^{66}\left( \cos \left( \frac{\pi }{3} \right)+i\sin \left( \frac{\pi }{3} \right) \right) \\
+
-
& =2^{66}\left( \frac{1}{2}+i\frac{\sqrt{3}}{2} \right)=2^{65}\left( 1+i\sqrt{3} \right) \\
+
-
\end{align}</math>
+

Aktuelle Version

Wir bringen zuerst \displaystyle 4\sqrt{3}-4i in Polarform und verwenden dann den Moivreschen Satz.

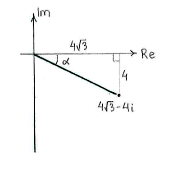
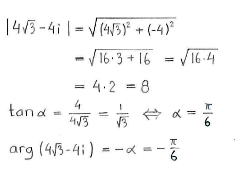
Image:3_3_1_c.gif Image:3_3_1_c_text.gif

Dies ergibt

\displaystyle 4\sqrt{3}-4i = 8\Bigl(\cos\Bigl(-\frac{\pi}{6}\Bigr) + i\sin\Bigl(-\frac{\pi}{6}\Bigr)\Bigr)

und durch den Moivreschen Satz erhalten wir

\displaystyle \begin{align}

\bigl(4\sqrt{3}-4i\bigr)^{22} &= 8^{22}\Bigl(\cos\Bigl(22\cdot\Bigl(-\frac{\pi}{6}\Bigr)\Bigr) + i\sin\Bigl(22\cdot\Bigl(-\frac{\pi}{6}\Bigr)\Bigr)\Bigr)\\[5pt] &= \bigl(2^3\bigr)^{22}\Bigl(\cos\Bigl(-\frac{11\pi}{3}\Bigr) + i\sin\Bigl(-\frac{11\pi}{3}\Bigr)\Bigr)\\[5pt] &= 2^{3\cdot 22}\Bigl(\cos\Bigl(-\frac{12\pi -\pi }{3}\Bigr) + i\sin\Bigl(-\frac{12\pi -\pi}{3}\Bigr)\Bigr)\\[5pt] &= 2^{66}\Bigl(\cos\Bigl(-4\pi+\frac{\pi}{3}\Bigr) + i\sin\Bigl(-4\pi+\frac{\pi}{3} \Bigr)\Bigr)\\[5pt] &= 2^{66}\Bigl(\cos\frac{\pi}{3} + i\sin\frac{\pi}{3}\Bigr)\\[5pt] &= 2^{66}\Bigl(\frac{1}{2} + i\frac{\sqrt{3}}{2}\Bigr)\\[5pt] &= 2^{65}(1+i\sqrt{3}\,)\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.3:1c“