Lösung 3.2:3

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Aktuelle Version (09:39, 18. Sep. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 6 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
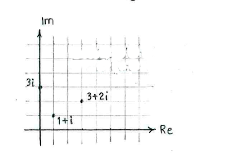
If we mark the three complex numbers in the plane, we see that the fourth corner will have
+
Zeichnen wir die drei Punkte in der komplexen Zahlenebene, so sehen wir, dass die vierte Ecke ein Punkt in der komplexen Zahlenebene ist, dessen Realteil zwischen 0 und 3 liegt, und dessen Imagin&auml;rteil gr&ouml;sser als 3 ist (der Punkt liegt oberhalb von <math> 0+3i </math>).
-
<math>\text{3}+\text{2}i</math>
+
-
and
+
-
<math>\text{3}i</math>
+
-
as neighbouring corners.
+
-
 
+
[[Image:3_2_3_1.gif|center]]
[[Image:3_2_3_1.gif|center]]
-
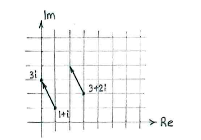
In order to find the fourth corner, we use the fact that in a square opposite sides are parallel and all sides have the same length. This means that the vector from
+
Um die vierte Ecke zu finden, benutzen wir, dass gegenüberliegende Seiten parallel sind und dieselbe Länge haben. Also ist der Vektor von <math>1+i</math> zu <math>3i</math> derselbe wir der Vektor von <math>3+2i</math> zum vierten Punkt.
-
<math>\text{1}+i</math>
+
-
to
+
-
<math>\text{3}i</math>
+
-
is equal to the vector from
+
-
<math>\text{3}+\text{2}i</math>
+
-
to the fourth corner.
+
-
 
+
[[Image:3_2_3_2.gif|center]]
[[Image:3_2_3_2.gif|center]]
-
If we interpret the complex numbers as vectors, this means that the vector from
+
Das bedeutet, dass der Vektor von
-
<math>\text{1}+i</math>
+
<math>1+i</math> bis <math>\text{3}i</math>
-
to
+
-
<math>\text{3}i</math>
+
-
is
+
-
 
+
-
 
+
-
<math>3i-\left( 1+i \right)=-1+2i</math>
+
 +
{{Abgesetzte Formel||<math>3i-(1+i) = -1+2i</math>}}
-
And we obtain the fourth corner if we add this vector to the corner
+
ist. Addieren wir diesen Vektor zum Punkt <math>3+2i</math>, erhalten wir die vierte Ecke,
-
<math>\text{3}+\text{2}i</math>,
+
 +
{{Abgesetzte Formel||<math>3+2i+(-1+2i) = 2+4i\,\textrm{.}</math>}}
-
<math>\text{3}+\text{2}i+\left( -1+2i \right)=2+4i</math>
+
Unsere anf&auml;nglichen Vermutungen haben sich best&auml;tigt: F&uuml;r den Realteil gilt: <math> 2 \in (0,3) </math> und f&uuml;r den Imagin&auml;rteil gilt: <math> 4 > 3 </math>.

Aktuelle Version

Zeichnen wir die drei Punkte in der komplexen Zahlenebene, so sehen wir, dass die vierte Ecke ein Punkt in der komplexen Zahlenebene ist, dessen Realteil zwischen 0 und 3 liegt, und dessen Imaginärteil grösser als 3 ist (der Punkt liegt oberhalb von \displaystyle 0+3i ).

Um die vierte Ecke zu finden, benutzen wir, dass gegenüberliegende Seiten parallel sind und dieselbe Länge haben. Also ist der Vektor von \displaystyle 1+i zu \displaystyle 3i derselbe wir der Vektor von \displaystyle 3+2i zum vierten Punkt.

Das bedeutet, dass der Vektor von \displaystyle 1+i bis \displaystyle \text{3}i

\displaystyle 3i-(1+i) = -1+2i

ist. Addieren wir diesen Vektor zum Punkt \displaystyle 3+2i, erhalten wir die vierte Ecke,

\displaystyle 3+2i+(-1+2i) = 2+4i\,\textrm{.}

Unsere anfänglichen Vermutungen haben sich bestätigt: Für den Realteil gilt: \displaystyle 2 \in (0,3) und für den Imaginärteil gilt: \displaystyle 4 > 3 .

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:3“