Lösung 2.1:4c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Aktuelle Version (11:02, 27. Aug. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 5 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
First, we need a picture of what the region looks like.
+
Zuerst betrachten wir den Graphen, der unser Gebiet einschließt.
-
 
+
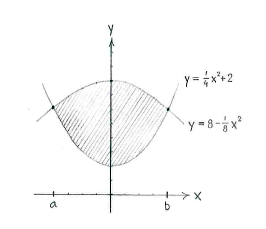
Die Kurven <math>y=x^2/4+2</math> und <math>y=8-x^2/8</math> sind beide quadratische Funktionen. Die erste hat ihr Minimum <math>y=2</math> wenn <math>x=0</math> und die zweite das Maximum <math>y=8</math> wenn <math>x=0</math>. Die Kurven sehen ungefähr wie im Bild unten aus.
-
Both curves,
+
-
<math>y=\frac{1}{4}x^{2}+2</math>
+
-
and
+
-
<math>y=8-\frac{1}{8}x^{2}</math>, are parabolas, the first with a minimum value
+
-
<math>y=\text{2}</math>
+
-
when
+
-
<math>x=0</math>, and the second with a maximum value of
+
-
<math>y=\text{8}</math>
+
-
when
+
-
<math>x=0</math>. Roughly speaking, the curves have the appearance shown in the figure below, where the shaded region whose area we are trying to find lies between the curves.
+
-
 
+
[[Image:2_1_4_c.gif|center]]
[[Image:2_1_4_c.gif|center]]
 +
Die obere Grenze der Fläche ist die Funktion <math>y=8-x^2/8</math> und die untere Grenze die Funktion <math>y=x^2/4+2</math>. Bestimmen wir die Schnittstellen <math>x=a</math> und <math>x=b</math> der beiden Kurven, ist die Fläche
-
The region is bounded above by the parabola
+
{{Abgesetzte Formel||<math>\text{Fläche} = \int\limits_{a}^{b} \bigl(\bigl(8-\tfrac{1}{8}x^2\bigr) - \bigl(\tfrac{1}{4}x^2+2\bigr)\bigr)\,dx\,\textrm{.}</math>}}
-
<math>y=8-\frac{1}{8}x^{2}</math>
+
-
and below by the parabola
+
-
<math>y=\frac{1}{4}x^{2}+2</math>. If we can determine the
+
-
<math>x</math>
+
-
-coordinates,
+
-
<math>x=a\text{ }</math>
+
-
and
+
-
<math>x=b</math>, for the points of intersection between the curves, the area we are looking for will be given by
+
-
Area =
+
Die Fläche ist das Integral der Differenz zwischen den beiden Funktionen.
-
<math>\int\limits_{a}^{b}{\left( \left( 8-\frac{1}{8}x^{2} \right)-\left( \frac{1}{4}x^{2}+2 \right) \right)}\,dx</math>
+
 +
Wir erhalten die Schnittstellen durch folgende Gleichung:
-
The integrand is the
+
{{Abgesetzte Formel||<math>\left\{\begin{align}
-
<math>y</math>
+
y &= 8-\tfrac{1}{8}x^2\,,\\[5pt]
-
-value for the upper parabola minus the corresponding
+
y &= \tfrac{1}{4}x^2+2\,\textrm{.}
-
<math>y</math>
+
\end{align}\right.</math>}}
-
-value for the lower parabola.
+
-
At the points where the curves intersect each other, the
+
Eliminieren wir ''y'' und lösen die Gleichung für ''x'', erhalten wir die Schnittstellen.
-
<math>x</math>
+
-
- and
+
-
<math>y</math>
+
-
-coordinates are equal, which gives the equation system,
+
-
 
+
{{Abgesetzte Formel||<math>8-\tfrac{1}{8}x^2 = \tfrac{1}{4}x^2+2\,</math>}}
-
<math>\left\{ \begin{matrix}
+
-
y=8-\frac{1}{8}x^{2} \\
+
-
y=\frac{1}{4}x^{2}+2 \\
+
-
\end{matrix} \right.</math>
+
-
 
+
-
 
+
-
If we eliminate
+
-
<math>y</math>
+
-
from this system, we get the following equation for
+
-
<math>x</math>,
+
-
 
+
-
 
+
-
<math>8-\frac{1}{8}x^{2}=\frac{1}{4}x^{2}+2</math>
+
 +
oder
-
If we move the
+
{{Abgesetzte Formel||<math>\tfrac{1}{4}x^2 + \tfrac{1}{8}x^2 = 8-2\,</math>,}}
-
<math>x^{2}</math>
+
-
terms onto one side and the constants onto the other, we obtain
+
-
 
+
-
 
+
-
<math>\frac{1}{4}x^{2}+\frac{1}{8}x^{2}=8-2</math>,
+
-
 
+
-
i.e.
+
-
 
+
-
 
+
-
<math>\begin{align}
+
-
& \left( \frac{1}{4}+\frac{1}{8} \right)x^{2}=6 \\
+
-
& \frac{3}{8}x^{2}=6 \\
+
-
& x^{2}=16 \\
+
-
\end{align}</math>
+
 +
also ist
-
The
+
{{Abgesetzte Formel||<math>\begin{align}
-
<math>x</math>
+
\bigl(\tfrac{1}{4}+\tfrac{1}{8}\bigr)x^2 &= 6\,\\[5pt]
-
-coordinates of the points of intersection are therefore equal to
+
\tfrac{3}{8}x^2 &= 6\,\\[5pt]
-
<math>x=-\text{4 }</math>
+
x^2 &= 16\,\textrm{.}
-
and
+
\end{align}</math>}}
-
<math>x=\text{4}</math>.
+
-
The area of the area between the curves is given by
+
Also sind die Schnittstellen <math>x=-4</math> und <math>x=4\,</math>.
 +
Die Fläche zwischen den Kurven ist also
-
<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
-
& \text{Area}=\int\limits_{-4}^{4}{\left( \left( 8-\frac{1}{8}x^{2} \right)-\left( \frac{1}{4}x^{2}+2 \right) \right)}\,dx \\
+
\text{Fläche} &= \int\limits_{-4}^{4} \Bigl(\Bigl(8-\frac{1}{8}x^2\Bigr)-\Bigl( \frac{1}{4}x^2+2\Bigr) \Bigr)\,dx\\[5pt]
-
& =\int\limits_{-4}^{4}{\left( 8-\frac{1}{8}x^{2}-\frac{1}{4}x^{2}-2 \right)}\,dx \\
+
&= \int\limits_{-4}^{4}\Bigl(8-\frac{1}{8}x^2-\frac{1}{4}x^2-2\Bigr)\,dx\\[5pt]
-
& =\int\limits_{-4}^{4}{\left( 6-\left( \frac{1}{8}+\frac{1}{4} \right)x^{2} \right)}\,dx \\
+
&= \int\limits_{-4}^{4}\Bigl(6-\Bigl(\frac{1}{8}+\frac{1}{4}\Bigr)x^2\Bigr)\,dx\\[5pt]
-
& =\int\limits_{-4}^{4}{\left( 6-\frac{3}{8}x^{2} \right)}\,dx \\
+
&= \int\limits_{-4}^{4}\Bigl(6-\frac{3}{8}x^2\Bigr)\,dx\\[5pt]
-
& =\left[ 6x-\frac{3}{8}\frac{x^{3}}{3} \right]_{-4}^{4} \\
+
&= \Bigl[\ 6x-\frac{3}{8}\frac{x^3}{3}\ \Bigr]_{-4}^{4}\\[5pt]
-
& =\left[ 6x-\frac{x^{3}}{8} \right]_{-4}^{4} \\
+
&= \Bigl[\ 6x-\frac{x^3}{8}\ \Bigr]_{-4}^{4}\\[5pt]
-
& =6\centerdot 4-\frac{4^{3}}{8}-\left( 6\left( -4 \right)-\frac{\left( -4 \right)^{3}}{8} \right) \\
+
&= 6\cdot 4 - \frac{4^3}{8} - \Bigl(6\cdot (-4) - \frac{(-4)^3}{8}\Bigr)\\[5pt]
-
& =24-8+24-8=32 \\
+
&= 24-8+24-8\\[5pt]
-
\end{align}</math>
+
&= 32\,\textrm{.}
 +
\end{align}</math>}}

Aktuelle Version

Zuerst betrachten wir den Graphen, der unser Gebiet einschließt. Die Kurven \displaystyle y=x^2/4+2 und \displaystyle y=8-x^2/8 sind beide quadratische Funktionen. Die erste hat ihr Minimum \displaystyle y=2 wenn \displaystyle x=0 und die zweite das Maximum \displaystyle y=8 wenn \displaystyle x=0. Die Kurven sehen ungefähr wie im Bild unten aus.

Die obere Grenze der Fläche ist die Funktion \displaystyle y=8-x^2/8 und die untere Grenze die Funktion \displaystyle y=x^2/4+2. Bestimmen wir die Schnittstellen \displaystyle x=a und \displaystyle x=b der beiden Kurven, ist die Fläche

\displaystyle \text{Fläche} = \int\limits_{a}^{b} \bigl(\bigl(8-\tfrac{1}{8}x^2\bigr) - \bigl(\tfrac{1}{4}x^2+2\bigr)\bigr)\,dx\,\textrm{.}

Die Fläche ist das Integral der Differenz zwischen den beiden Funktionen.

Wir erhalten die Schnittstellen durch folgende Gleichung:

\displaystyle \left\{\begin{align} 
y &= 8-\tfrac{1}{8}x^2\,,\\[5pt]
y &= \tfrac{1}{4}x^2+2\,\textrm{.}

\end{align}\right.

Eliminieren wir y und lösen die Gleichung für x, erhalten wir die Schnittstellen.

\displaystyle 8-\tfrac{1}{8}x^2 = \tfrac{1}{4}x^2+2\,

oder

\displaystyle \tfrac{1}{4}x^2 + \tfrac{1}{8}x^2 = 8-2\,,

also ist

\displaystyle \begin{align}

\bigl(\tfrac{1}{4}+\tfrac{1}{8}\bigr)x^2 &= 6\,\\[5pt] \tfrac{3}{8}x^2 &= 6\,\\[5pt] x^2 &= 16\,\textrm{.} \end{align}

Also sind die Schnittstellen \displaystyle x=-4 und \displaystyle x=4\,.

Die Fläche zwischen den Kurven ist also

\displaystyle \begin{align}

\text{Fläche} &= \int\limits_{-4}^{4} \Bigl(\Bigl(8-\frac{1}{8}x^2\Bigr)-\Bigl( \frac{1}{4}x^2+2\Bigr) \Bigr)\,dx\\[5pt] &= \int\limits_{-4}^{4}\Bigl(8-\frac{1}{8}x^2-\frac{1}{4}x^2-2\Bigr)\,dx\\[5pt] &= \int\limits_{-4}^{4}\Bigl(6-\Bigl(\frac{1}{8}+\frac{1}{4}\Bigr)x^2\Bigr)\,dx\\[5pt] &= \int\limits_{-4}^{4}\Bigl(6-\frac{3}{8}x^2\Bigr)\,dx\\[5pt] &= \Bigl[\ 6x-\frac{3}{8}\frac{x^3}{3}\ \Bigr]_{-4}^{4}\\[5pt] &= \Bigl[\ 6x-\frac{x^3}{8}\ \Bigr]_{-4}^{4}\\[5pt] &= 6\cdot 4 - \frac{4^3}{8} - \Bigl(6\cdot (-4) - \frac{(-4)^3}{8}\Bigr)\\[5pt] &= 24-8+24-8\\[5pt] &= 32\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:4c“