Lösung 3.2:1b
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
K (Lösning 3.2:1b moved to Solution 3.2:1b: Robot: moved page) |
|||
| (Der Versionsvergleich bezieht 4 dazwischen liegende Versionen mit ein.) | |||
| Zeile 1: | Zeile 1: | ||
| - | + | Wir können einfach<math>z+u</math> und <math>z-u</math> berechnen, | |
| - | < | + | |
| - | + | ||
| - | + | ||
| - | < | + | |
| - | + | ||
| + | {{Abgesetzte Formel||<math>\begin{align} | ||
| + | z+u &= 2+i+(-1-2i) = 2-1+(1-2)i = 1-i,\\[5pt] | ||
| + | z-u &= 2+i-(-1-2i) = 2+1+(1+2)i = 3+3i, | ||
| + | \end{align}</math>}} | ||
| + | |||
| + | und in der komplexen Zahlenebene einzeichnen. | ||
| + | |||
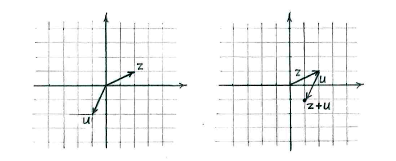
| + | Alternativ konnen wir <math>z</math> und <math>u</math> als Vektoren betrachten, und <math>z+u</math> wir die Addition von den Vektoren <math>z</math> und <math>u</math> sehen. | ||
[[Image:3_2_1_b1.gif|center]] | [[Image:3_2_1_b1.gif|center]] | ||
| + | |||
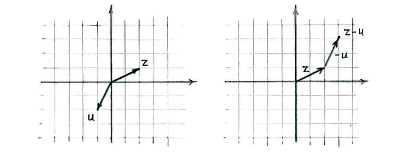
| + | Wir können entweder <math>z-u</math> als <math>z+(-u)</math> interpretieren, | ||
[[Image:3_2_1_b2.gif|center]] | [[Image:3_2_1_b2.gif|center]] | ||
| + | |||
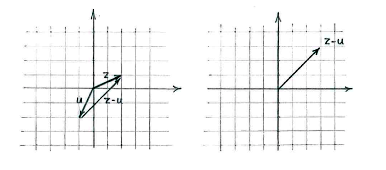
| + | oder <math>z-u</math> von der Gleichung | ||
| + | |||
| + | {{Abgesetzte Formel||<math>z=(z-u)+u\,,</math>}} | ||
| + | |||
| + | erhalten, wo also <math>z-u</math> der Vektor ist, den wir zu <math>u</math> addieren um <math>z</math> zu erhalten. | ||
[[Image:3_2_1_b3.gif|center]] | [[Image:3_2_1_b3.gif|center]] | ||
Aktuelle Version
Wir können einfach\displaystyle z+u und \displaystyle z-u berechnen,
| \displaystyle \begin{align}
z+u &= 2+i+(-1-2i) = 2-1+(1-2)i = 1-i,\\[5pt] z-u &= 2+i-(-1-2i) = 2+1+(1+2)i = 3+3i, \end{align} |
und in der komplexen Zahlenebene einzeichnen.
Alternativ konnen wir \displaystyle z und \displaystyle u als Vektoren betrachten, und \displaystyle z+u wir die Addition von den Vektoren \displaystyle z und \displaystyle u sehen.
Wir können entweder \displaystyle z-u als \displaystyle z+(-u) interpretieren,
oder \displaystyle z-u von der Gleichung
| \displaystyle z=(z-u)+u\,, |
erhalten, wo also \displaystyle z-u der Vektor ist, den wir zu \displaystyle u addieren um \displaystyle z zu erhalten.