Aus Online Mathematik Brückenkurs 2

Version vom 07:58, 21. Aug. 2008 (bearbeiten) Tekbot (Diskussion | Beiträge) K (Robot: Automated text replacement (-[[Bild: +[[Image:)) ← Zum vorherigen Versionsunterschied		Aktuelle Version (10:47, 27. Aug. 2009) (bearbeiten) (rückgängig) Sekretariat1 (Diskussion | Beiträge)
(Der Versionsvergleich bezieht 9 dazwischen liegende Versionen mit ein.)
Zeile 1:		Zeile 1:
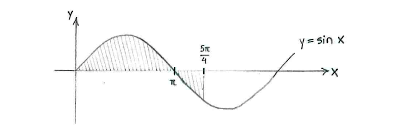
-	{{NAVCONTENT_START}}	+	Zeichnen wir die Funktion <math>y=\sin x</math>, sehen wir, dass die Funktion bis <math>x=\pi </math> oberhalb der ''x''-Achse liegt und danach unterhalb.
-	<center> [[Image:2_1_4a-1(2).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	[[Image:2_1_4_a1.gif|center]]
-	{{NAVCONTENT_START}}	+
-	<center> [[Image:2_1_4a-2(2).gif]] </center>	+	Die Fläche vom Gebiet zwischen <math>x=0</math> und <math>x=\pi</math> ist deshalb
-	{{NAVCONTENT_STOP}}	+
		+	{{Abgesetzte Formel||<math>\int\limits_{0}^{\pi} \sin x\,dx</math>}}
		+
		+	während die Fläche vom restierenden Gebiet
		+
		+	{{Abgesetzte Formel||<math>-\int\limits_{\pi}^{5\pi/4} \sin x\,dx\textrm{,}</math>}}
		+
		+	ist (beachte das Minuszeichen).
		+
		+	Die gesamte Fläche ist also
		+
		+	{{Abgesetzte Formel||<math>\begin{align}
		+	& \int\limits_{0}^{\pi} \sin x\,dx - \int\limits_{\pi}^{5\pi/4} \sin x\,dx\\[5pt]
		+	&\qquad\quad {}= \Bigl[\ -\cos x\ \Bigr]_0^\pi - \Bigl[\ -\cos x\ \Bigr]_\pi^{5\pi/4}\\[5pt]
		+	&\qquad\quad {}= \Bigl( -\cos\pi - (-\cos 0)\Bigr) - \Bigl( -\cos\frac{5\pi}{4} - (-\cos\pi) \Bigr)\\[5pt]
		+	&\qquad\quad {}= \Bigl( -(-1)-(-1) \Bigr) - \Bigl( -\Bigl(-\frac{1}{\sqrt{2}} \Bigr) - \bigl(-(-1)\bigr)\Bigr)\\[5pt]
		+	&\qquad\quad {}= 1+1-\frac{1}{\sqrt{2}}+1\\[5pt]
		+	&\qquad\quad {}= 3-\frac{1}{\sqrt{2}}\,\textrm{.}
		+	\end{align}</math>}}
		+
		+	Hinweis: Die exakten Werte von <math>\cos 0</math>, <math>\cos \pi </math> und <math>\cos (5\pi/4)</math> können wir durch den Einheitskreis erhalten, indem wir die Winkeln <math>0</math>, <math>\pi</math> und <math>5\pi/4</math> einzeichnen und deren ''x''-Koordinaten ablesen.
		+
		+	[[Image:2_1_4_a2.gif|center]]

---

Aktuelle Version

Zeichnen wir die Funktion \displaystyle y=\sin x, sehen wir, dass die Funktion bis \displaystyle x=\pi oberhalb der x-Achse liegt und danach unterhalb.

Die Fläche vom Gebiet zwischen \displaystyle x=0 und \displaystyle x=\pi ist deshalb

\displaystyle \int\limits_{0}^{\pi} \sin x\,dx

während die Fläche vom restierenden Gebiet

\displaystyle -\int\limits_{\pi}^{5\pi/4} \sin x\,dx\textrm{,}

ist (beachte das Minuszeichen).

Die gesamte Fläche ist also

\displaystyle \begin{align} & \int\limits_{0}^{\pi} \sin x\,dx - \int\limits_{\pi}^{5\pi/4} \sin x\,dx\\[5pt] &\qquad\quad {}= \Bigl[\ -\cos x\ \Bigr]_0^\pi - \Bigl[\ -\cos x\ \Bigr]_\pi^{5\pi/4}\\[5pt] &\qquad\quad {}= \Bigl( -\cos\pi - (-\cos 0)\Bigr) - \Bigl( -\cos\frac{5\pi}{4} - (-\cos\pi) \Bigr)\\[5pt] &\qquad\quad {}= \Bigl( -(-1)-(-1) \Bigr) - \Bigl( -\Bigl(-\frac{1}{\sqrt{2}} \Bigr) - \bigl(-(-1)\bigr)\Bigr)\\[5pt] &\qquad\quad {}= 1+1-\frac{1}{\sqrt{2}}+1\\[5pt] &\qquad\quad {}= 3-\frac{1}{\sqrt{2}}\,\textrm{.} \end{align}

Hinweis: Die exakten Werte von \displaystyle \cos 0, \displaystyle \cos \pi und \displaystyle \cos (5\pi/4) können wir durch den Einheitskreis erhalten, indem wir die Winkeln \displaystyle 0, \displaystyle \pi und \displaystyle 5\pi/4 einzeichnen und deren x-Koordinaten ablesen.