Lösung 3.2:5a
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
K (Lösning 3.2:5a moved to Solution 3.2:5a: Robot: moved page) |
|||
| (Der Versionsvergleich bezieht 4 dazwischen liegende Versionen mit ein.) | |||
| Zeile 1: | Zeile 1: | ||
| - | + | Das Argument einer komplexen Zahl ist der Winkel zwischen der Zahl und der positiven reellen Achse, gegen den Uhrzeigersinn. | |
| - | < | + | |
| - | + | In diesem Fall sehen wir direkt dass das Winkel von <math>-10</math>, <math>\pi</math> ist. | |
[[Image:3_2_5_a.gif|center]] | [[Image:3_2_5_a.gif|center]] | ||
| + | |||
| + | Hinweis: Alle Argumente die sich nur mit ein Vielfaches von <math>2\pi</math> unterscheiden, beschreiben bekanntlich denselben Winkel. Also hätten wir auch mit <math>-\pi</math>, <math>3\pi</math>, <math>5\pi</math> etc antworten können. Meistens antwortet man aber mit einen Winkel entweder zwischen <math>0</math> und <math>2\pi</math> oder zwischen <math>-\pi</math> und <math>\pi</math>. | ||
Aktuelle Version
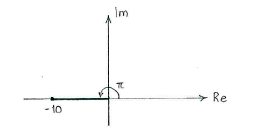
Das Argument einer komplexen Zahl ist der Winkel zwischen der Zahl und der positiven reellen Achse, gegen den Uhrzeigersinn.
In diesem Fall sehen wir direkt dass das Winkel von \displaystyle -10, \displaystyle \pi ist.
Hinweis: Alle Argumente die sich nur mit ein Vielfaches von \displaystyle 2\pi unterscheiden, beschreiben bekanntlich denselben Winkel. Also hätten wir auch mit \displaystyle -\pi, \displaystyle 3\pi, \displaystyle 5\pi etc antworten können. Meistens antwortet man aber mit einen Winkel entweder zwischen \displaystyle 0 und \displaystyle 2\pi oder zwischen \displaystyle -\pi und \displaystyle \pi.