Aus Online Mathematik Brückenkurs 2

Version vom 10:52, 3. Okt. 2008 (bearbeiten) Jamesjmnewton (Diskussion | Beiträge) ← Zum vorherigen Versionsunterschied		Aktuelle Version (16:47, 14. Sep. 2009) (bearbeiten) (rückgängig) Silke2 (Diskussion | Beiträge) (Grammatik)
(Der Versionsvergleich bezieht 4 dazwischen liegende Versionen mit ein.)
Zeile 1:		Zeile 1:
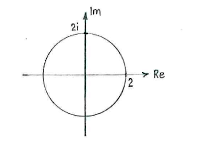
-	{{NAVCONTENT_START}}	+	Der Betrag <math>|z|</math> von der komplexen Zahl <math>z</math> ist dasselbe wie der Abstand zwischen <math>z</math> und <math>(0,0)</math>. Das <math>|z|=2</math> bedeutet also, dass die Zahlen <math>z</math>, die die Gleichung erfüllen, auf einem Kreis mit dem Mittelpunkt <math>(0,0)</math> und dem Radius 2 liegen.
-	The magnitude <math>|z|</math> of a complex number <math>z</math> is equal to the number's distance from the origin. The condition <math>|z|=2</math> therefore says that <math>z</math>'s distance from the origin should be <math>2</math>, i.e. the condition gives a circle of radius <math>2</math> and centre at the origin.	+
	[[Image:3_2_2_c_.gif|center]]		[[Image:3_2_2_c_.gif|center]]
-
-	{{NAVCONTENT_STOP}}

---

Aktuelle Version

Der Betrag \displaystyle |z| von der komplexen Zahl \displaystyle z ist dasselbe wie der Abstand zwischen \displaystyle z und \displaystyle (0,0). Das \displaystyle |z|=2 bedeutet also, dass die Zahlen \displaystyle z, die die Gleichung erfüllen, auf einem Kreis mit dem Mittelpunkt \displaystyle (0,0) und dem Radius 2 liegen.