Lösung 2.1:4e

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Robot: Automated text replacement (-[[Bild: +[[Image:))
Aktuelle Version (11:23, 27. Aug. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 8 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
Die doppelte Ungleichung bedeutet, dass ''y'' zwischen den Kurven <math>y=x+2</math> und <math>y=x^2</math> liegt.
-
<center> [[Image:2_1_4e-1(3).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
In der Figur unten ist das Gebiet eingezeichnet.
-
{{NAVCONTENT_START}}
+
 
-
<center> [[Image:2_1_4e-2(3).gif]] </center>
+
[[Image:2_1_4_e.gif|center]]
-
{{NAVCONTENT_STOP}}
+
 
-
{{NAVCONTENT_START}}
+
Die Fläche des Gebietes ist
-
<center> [[Image:2_1_4e-3(3).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
{{Abgesetzte Formel||<math>\text{Fläche} = \int\limits_a^b \bigl(x+2-x^2\bigr)\,dx\,\textrm{,}</math>}}
 +
 
 +
wobei <math>x=a</math> und <math>x=b</math> die Schnittstellen der beiden Kurven sind, die wir durch folgende Gleichung erhalten
 +
 
 +
{{Abgesetzte Formel||<math>\left\{\begin{align}
 +
y &= x+2\,,\\[5pt]
 +
y &= x^2\,\textrm{.}
 +
\end{align} \right.</math>}}
 +
 
 +
Eliminieren wir <math>y</math>, erhalten wir für <math>x</math> diese Gleichung
 +
 +
{{Abgesetzte Formel||<math>x^{2}=x+2\,\textrm{.}</math>}}
 +
 
 +
Hohlen wir alle ''x''-Terme zu einer Seite erhalten wir
 +
 
 +
{{Abgesetzte Formel||<math>x^2-x=2\,</math>.}}
 +
 
 +
Durch quadratische Ergänzung ergibt sich
 +
 
 +
{{Abgesetzte Formel||<math>\begin{align}
 +
\Bigl(x-\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 &= 2\\[5pt]
 +
\Bigl(x-\frac{1}{2}\Bigr)^2 &= \frac{9}{4}\,\textrm{.}
 +
\end{align}</math>}}
 +
 
 +
Wir erhalten also die Wurzeln <math>x=\tfrac{1}{2}\pm \tfrac{3}{2}</math>, oder <math>x=-1</math> und <math>x=2\,</math>.
 +
 
 +
Die Fläche ist also
 +
 
 +
{{Abgesetzte Formel||<math>\begin{align}
 +
\text{Fläche}
 +
&= \int\limits_{-1}^2 \bigl(x+2-x^2\bigr)\,dx\\[5pt]
 +
&= \Bigl[\ \frac{x^2}{2} + 2x - \frac{x^3}{3}\ \Bigr]_{-1}^2\\[5pt]
 +
&= \frac{2^2}{2} + 2\cdot 2 - \frac{2^3}{3} - \Bigl( \frac{(-1)^2}{2} + 2\cdot (-1) - \frac{(-1)^3}{3}\Bigr)\\[5pt]
 +
&= 2 + 4 - \frac{8}{3} - \frac{1}{2} + 2 - \frac{1}{3}\\[5pt]
 +
&= \frac{9}{2}\,\textrm{.}
 +
\end{align}</math>}}

Aktuelle Version

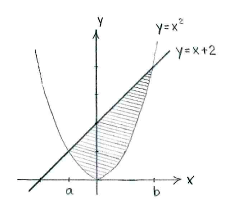
Die doppelte Ungleichung bedeutet, dass y zwischen den Kurven \displaystyle y=x+2 und \displaystyle y=x^2 liegt.

In der Figur unten ist das Gebiet eingezeichnet.

Die Fläche des Gebietes ist

\displaystyle \text{Fläche} = \int\limits_a^b \bigl(x+2-x^2\bigr)\,dx\,\textrm{,}

wobei \displaystyle x=a und \displaystyle x=b die Schnittstellen der beiden Kurven sind, die wir durch folgende Gleichung erhalten

\displaystyle \left\{\begin{align}

y &= x+2\,,\\[5pt] y &= x^2\,\textrm{.} \end{align} \right.

Eliminieren wir \displaystyle y, erhalten wir für \displaystyle x diese Gleichung

\displaystyle x^{2}=x+2\,\textrm{.}

Hohlen wir alle x-Terme zu einer Seite erhalten wir

\displaystyle x^2-x=2\,.

Durch quadratische Ergänzung ergibt sich

\displaystyle \begin{align}

\Bigl(x-\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 &= 2\\[5pt] \Bigl(x-\frac{1}{2}\Bigr)^2 &= \frac{9}{4}\,\textrm{.} \end{align}

Wir erhalten also die Wurzeln \displaystyle x=\tfrac{1}{2}\pm \tfrac{3}{2}, oder \displaystyle x=-1 und \displaystyle x=2\,.

Die Fläche ist also

\displaystyle \begin{align}

\text{Fläche} &= \int\limits_{-1}^2 \bigl(x+2-x^2\bigr)\,dx\\[5pt] &= \Bigl[\ \frac{x^2}{2} + 2x - \frac{x^3}{3}\ \Bigr]_{-1}^2\\[5pt] &= \frac{2^2}{2} + 2\cdot 2 - \frac{2^3}{3} - \Bigl( \frac{(-1)^2}{2} + 2\cdot (-1) - \frac{(-1)^3}{3}\Bigr)\\[5pt] &= 2 + 4 - \frac{8}{3} - \frac{1}{2} + 2 - \frac{1}{3}\\[5pt] &= \frac{9}{2}\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:4e“