Aus Online Mathematik Brückenkurs 2

Version vom 14:38, 16. Sep. 2008 (bearbeiten) Tekbot (Diskussion | Beiträge) K (Lösning 2.1:4b moved to Solution 2.1:4b: Robot: moved page) ← Zum vorherigen Versionsunterschied		Aktuelle Version (10:54, 27. Aug. 2009) (bearbeiten) (rückgängig) Sekretariat1 (Diskussion | Beiträge)
(Der Versionsvergleich bezieht 6 dazwischen liegende Versionen mit ein.)
Zeile 1:		Zeile 1:
-	{{NAVCONTENT_START}}	+	Durch quadratische Ergänzung erhalten wir
-	<center> [[Image:2_1_4b-1(4).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+
-	{{NAVCONTENT_START}}	+
-	<center> [[Image:2_1_4b-2(4).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+
-	{{NAVCONTENT_START}}	+
-	<center> [[Image:2_1_4b-3(4).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+
-	{{NAVCONTENT_START}}	+
-	<center> [[Image:2_1_4b-4(4).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+
		+	{{Abgesetzte Formel||<math>\begin{align}
		+	y &= -x^2 + 2x + 2\\[5pt]
		+	&= -\bigl(x^2 - 2x- 2\bigr)\\[5pt]
		+	&= -\bigl((x-1)^2 - 1^2 - 2\bigr)\\[5pt]
		+	&= -(x-1)^2 + 3 \textrm{.}
		+	\end{align}</math>}}
		+
		+	Wir sehen, dass die Funktion eine Parabel mit dem Maximum <math>y=3</math> bei <math>x=1</math> ist.
	[[Image:2_1_4_b.gif|center]]		[[Image:2_1_4_b.gif|center]]
		+
		+	Die Fläche, die wir bestimmen sollen, ist im Bild schraffiert.
		+
		+	Diese Fläche bestimmen wir mit dem Integral
		+
		+	{{Abgesetzte Formel||<math>\text{Fläche} = \int\limits_a^b \bigl(-x^2+2x+2\bigr)\,dx\,,</math>}}
		+
		+	wobei ''a'' und ''b'' die Schnittstellen der Parabel und der ''x''-Achse sind, also die Wurzeln von
		+
		+	{{Abgesetzte Formel||<math>0=-x^{2}+2x+2</math>}}
		+
		+	oder, durch quadratische Ergänzung (siehe oben)
		+
		+	{{Abgesetzte Formel||<math>0=-(x-1)^2+3 \textrm{,}</math>}}
		+
		+	also
		+
		+	{{Abgesetzte Formel||<math>(x-1)^2=3\,\textrm{.}</math>}}
		+
		+	Die Gleichung hat also die Wurzeln <math>x = 1\pm \sqrt{3}\</math> , <math>x=1-\sqrt{3}</math> und <math>x=1+\sqrt{3}\</math>.
		+
		+	Die Fläche ist also
		+
		+	{{Abgesetzte Formel||<math>\text{Fläche} = \int\limits_{1-\sqrt{3}}^{1+\sqrt{3}} \bigl(-x^2+2x+2\bigr)\,dx\,\textrm{.}</math>}}
		+
		+	Wir schreiben hier den Integranden in die quadratisch ergänzte Form.
		+
		+	{{Abgesetzte Formel||<math>\text{Fläche} = \int\limits_{1-\sqrt{3}}^{1+\sqrt{3}} \bigl( -(x-1)^2 + 3\bigr)\,dx\,,</math>}}
		+
		+	So erhalten wir die Stammfunktion
		+
		+	{{Abgesetzte Formel||<math>\text{Fläche} = \Bigl[\ -\frac{(x-1)^3}{3} + 3x\ \Bigr]_{1-\sqrt{3}}^{1+\sqrt{3}}\,</math>.}}
		+
		+	Daraus folgt
		+
		+	{{Abgesetzte Formel||<math>\begin{align}
		+	\text{Fläche} &= -\frac{(1+\sqrt{3}-1)^3}{3}+3(1+\sqrt{3}\,)-\Bigl(-\frac{(1-\sqrt{3}-1)^3}{3}+3(1-\sqrt{3}\,)\Bigr)\\[5pt]
		+	&= -\frac{(\sqrt{3}\,)^3}{3} + 3 + 3\sqrt{3} + \frac{(-\sqrt{3}\,)^3}{3} - 3 + 3\sqrt{3}\\[5pt]
		+	&= -\frac{\sqrt{3}\sqrt{3}\sqrt{3}}{3} + 3\sqrt{3} + \frac{(-\sqrt{3}\,)(-\sqrt{3}\,)(-\sqrt{3}\,)}{3} + 3\sqrt{3}\\[5pt]
		+	&= -\frac{3\sqrt{3}}{3} + 3\sqrt{3} - \frac{3\sqrt{3}}{3} + 3\sqrt{3}\\[5pt]
		+	&= -\sqrt{3} + 3\sqrt{3} - \sqrt{3} + 3\sqrt{3}\\[5pt]
		+	&= (-1+3-1+3)\sqrt{3}\\[5pt]
		+	&= 4\sqrt{3}\,\textrm{.}
		+	\end{align}</math>}}
		+
		+	Hinweis: Die Rechnungen werden umständlich, wenn wir mit dem Ausdruck
		+
		+	{{Abgesetzte Formel||<math>\int\limits_{1-\sqrt{3}}^{1+\sqrt{3}}{\bigl(-x^2+2x+2 \bigr)}\,dx = \cdots</math>}}
		+
		+	rechnen.

---

Aktuelle Version

Durch quadratische Ergänzung erhalten wir

\displaystyle \begin{align} y &= -x^2 + 2x + 2\\[5pt] &= -\bigl(x^2 - 2x- 2\bigr)\\[5pt] &= -\bigl((x-1)^2 - 1^2 - 2\bigr)\\[5pt] &= -(x-1)^2 + 3 \textrm{.} \end{align}

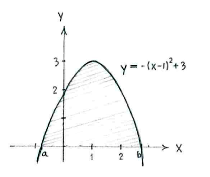
Wir sehen, dass die Funktion eine Parabel mit dem Maximum \displaystyle y=3 bei \displaystyle x=1 ist.

Die Fläche, die wir bestimmen sollen, ist im Bild schraffiert.

Diese Fläche bestimmen wir mit dem Integral

\displaystyle \text{Fläche} = \int\limits_a^b \bigl(-x^2+2x+2\bigr)\,dx\,,

wobei a und b die Schnittstellen der Parabel und der x-Achse sind, also die Wurzeln von

\displaystyle 0=-x^{2}+2x+2

oder, durch quadratische Ergänzung (siehe oben)

\displaystyle 0=-(x-1)^2+3 \textrm{,}

also

\displaystyle (x-1)^2=3\,\textrm{.}

Die Gleichung hat also die Wurzeln \displaystyle x = 1\pm \sqrt{3}\ , \displaystyle x=1-\sqrt{3} und \displaystyle x=1+\sqrt{3}\.

Die Fläche ist also

\displaystyle \text{Fläche} = \int\limits_{1-\sqrt{3}}^{1+\sqrt{3}} \bigl(-x^2+2x+2\bigr)\,dx\,\textrm{.}

Wir schreiben hier den Integranden in die quadratisch ergänzte Form.

\displaystyle \text{Fläche} = \int\limits_{1-\sqrt{3}}^{1+\sqrt{3}} \bigl( -(x-1)^2 + 3\bigr)\,dx\,,

So erhalten wir die Stammfunktion

\displaystyle \text{Fläche} = \Bigl[\ -\frac{(x-1)^3}{3} + 3x\ \Bigr]_{1-\sqrt{3}}^{1+\sqrt{3}}\,.

Daraus folgt

\displaystyle \begin{align} \text{Fläche} &= -\frac{(1+\sqrt{3}-1)^3}{3}+3(1+\sqrt{3}\,)-\Bigl(-\frac{(1-\sqrt{3}-1)^3}{3}+3(1-\sqrt{3}\,)\Bigr)\\[5pt] &= -\frac{(\sqrt{3}\,)^3}{3} + 3 + 3\sqrt{3} + \frac{(-\sqrt{3}\,)^3}{3} - 3 + 3\sqrt{3}\\[5pt] &= -\frac{\sqrt{3}\sqrt{3}\sqrt{3}}{3} + 3\sqrt{3} + \frac{(-\sqrt{3}\,)(-\sqrt{3}\,)(-\sqrt{3}\,)}{3} + 3\sqrt{3}\\[5pt] &= -\frac{3\sqrt{3}}{3} + 3\sqrt{3} - \frac{3\sqrt{3}}{3} + 3\sqrt{3}\\[5pt] &= -\sqrt{3} + 3\sqrt{3} - \sqrt{3} + 3\sqrt{3}\\[5pt] &= (-1+3-1+3)\sqrt{3}\\[5pt] &= 4\sqrt{3}\,\textrm{.} \end{align}

Hinweis: Die Rechnungen werden umständlich, wenn wir mit dem Ausdruck

\displaystyle \int\limits_{1-\sqrt{3}}^{1+\sqrt{3}}{\bigl(-x^2+2x+2 \bigr)}\,dx = \cdots

rechnen.