Lösung 3.3:6
Aus Online Mathematik Brückenkurs 2
| Zeile 1: | Zeile 1: | ||
| - | ''' | + | '''Polarform''' |
Wir lösen die Gleichung zuerst in Polarform, | Wir lösen die Gleichung zuerst in Polarform, | ||
| Zeile 12: | Zeile 12: | ||
{{Abgesetzte Formel||<math>r^2(\cos 2\alpha + i\sin 2\alpha) = \sqrt{2}\Bigl(\cos \frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>r^2(\cos 2\alpha + i\sin 2\alpha) = \sqrt{2}\Bigl(\cos \frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,\textrm{.}</math>}} | ||
| - | Damit die beiden Seiten gleich | + | Damit die beiden Seiten gleich sind, müssen die Beträge der beiden Seiten gleich sein und die Argumente der beiden Seiten dürfen sich nur um ein Multipel von <math>2\pi</math> unterscheiden, |
{{Abgesetzte Formel||<math>\left\{\begin{align} | {{Abgesetzte Formel||<math>\left\{\begin{align} | ||
| Zeile 26: | Zeile 26: | ||
\end{align}\right.</math>}} | \end{align}\right.</math>}} | ||
| - | Dies entspricht zwei Lösungen, nachdem alle geraden Zahlen | + | Dies entspricht zwei Lösungen, nachdem alle geraden Zahlen dem Argument <math>\pi/8</math> entsprechen, plus ein Multipel von <math>2\pi</math>, und alle ungerade Zahlen dem Argument <math>9\pi/8</math> entsprechen, plus ein Multipel von <math>2\pi</math>. |
In Polarform lauten die Lösungen also | In Polarform lauten die Lösungen also | ||
| Zeile 36: | Zeile 36: | ||
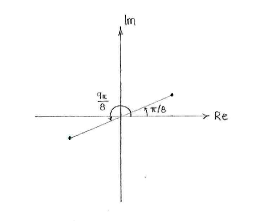
| - | Eine Lösung, <math>z=\sqrt[4]{2}(\cos (\pi/8) + i\sin (\pi/8)</math> liegt im ersten Quadrant | + | Eine Lösung, <math>z=\sqrt[4]{2}(\cos (\pi/8) + i\sin (\pi/8)</math> liegt im ersten Quadrant und die zweite Lösung, <math>z=\sqrt[4]{2}(\cos (9\pi/8) + i\sin (9\pi/8))</math> liegt im dritten Quadrant. |
[[Image:3_3_6.gif|center]] | [[Image:3_3_6.gif|center]] | ||
| Zeile 97: | Zeile 97: | ||
|} | |} | ||
| - | und wir erhalten | + | und wir erhalten, |
{{Abgesetzte Formel||<math>x=\pm \sqrt{\frac{\sqrt{2}+1}{2}}\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>x=\pm \sqrt{\frac{\sqrt{2}+1}{2}}\,\textrm{.}</math>}} | ||
| Zeile 127: | Zeile 127: | ||
|} | |} | ||
| - | und wir erhalten | + | und wir erhalten, |
{{Abgesetzte Formel||<math>y=\pm \sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>y=\pm \sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}</math>}} | ||
| Zeile 153: | Zeile 153: | ||
\end{align} \right.</math>}} | \end{align} \right.</math>}} | ||
| - | Die zweite Gleichung sagt dass <math>xy</math> positiv sein soll, und wir behalten daher nur die Gleichungen | + | Die zweite Gleichung sagt auch, dass <math>xy</math> positiv sein soll, und wir behalten daher nur die Gleichungen |
{{Abgesetzte Formel||<math>\left\{\begin{align} | {{Abgesetzte Formel||<math>\left\{\begin{align} | ||
| Zeile 165: | Zeile 165: | ||
\end{align}\right.</math>}} | \end{align}\right.</math>}} | ||
| - | Nachdem wir wissen dass unsere Gleichung zwei Lösungen hat, müssen dies unsere Lösungen sein: | + | Nachdem wir wissen, dass unsere Gleichung zwei Lösungen hat, müssen dies unsere Lösungen sein: |
{{Abgesetzte Formel||<math>z = \left\{\begin{align} | {{Abgesetzte Formel||<math>z = \left\{\begin{align} | ||
| Zeile 185: | Zeile 185: | ||
und wir erhalten auch | und wir erhalten auch | ||
| - | {{Abgesetzte Formel||<math>\tan\frac{\pi}{8} = \frac{\sin\dfrac{\pi}{8}}{\cos\dfrac{\pi}{8}} = \frac{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}-1}{2}}}{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}+1}{2}}} = \sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\,\textrm{.}</math>}} | + | {{Abgesetzte Formel||<math>\tan\frac{\pi}{8} = \frac{\sin\dfrac{\pi}{8}}{\cos\dfrac{\pi}{8}} = \frac{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}-1}{2}}}{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}+1}{2}}} = \sqrt {\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\,\textrm{.}</math>}} |
Wir können diesen Ausdruck vereinfachen, indem wir den Ausdruck mit den konjugieren Nenner erweitern, | Wir können diesen Ausdruck vereinfachen, indem wir den Ausdruck mit den konjugieren Nenner erweitern, | ||
| Zeile 191: | Zeile 191: | ||
{{Abgesetzte Formel||<math>\begin{align} | {{Abgesetzte Formel||<math>\begin{align} | ||
\tan\frac{\pi}{8} | \tan\frac{\pi}{8} | ||
| - | &= \sqrt{\frac{(\sqrt{2}-1)(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}} | + | &= \sqrt {\frac{(\sqrt{2}-1)(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}} |
| - | = \sqrt{\frac{(\sqrt{2}-1)^2}{(\sqrt{2})^2-1^2}}\\[5pt] | + | = \sqrt {\frac{(\sqrt{2}-1)^2}{(\sqrt{2})^2-1^2}}\\[5pt] |
&= \sqrt{\frac{(\sqrt{2}-1)^2}{2-1}} | &= \sqrt{\frac{(\sqrt{2}-1)^2}{2-1}} | ||
= \sqrt{(\sqrt{2}-1)^2} | = \sqrt{(\sqrt{2}-1)^2} | ||
= \sqrt{2}-1\,\textrm{.} | = \sqrt{2}-1\,\textrm{.} | ||
\end{align}</math>}} | \end{align}</math>}} | ||
Version vom 10:14, 23. Aug. 2009
Polarform
Wir lösen die Gleichung zuerst in Polarform,
| \displaystyle \begin{align}
z &= r\,(\cos\alpha + i\sin\alpha)\,,\\[5pt] 1+i &= \sqrt{2}\Bigl(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,, \end{align} |
und durch den Moivrischen Satz erhalten wir die Gleichung
| \displaystyle r^2(\cos 2\alpha + i\sin 2\alpha) = \sqrt{2}\Bigl(\cos \frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,\textrm{.} |
Damit die beiden Seiten gleich sind, müssen die Beträge der beiden Seiten gleich sein und die Argumente der beiden Seiten dürfen sich nur um ein Multipel von \displaystyle 2\pi unterscheiden,
| \displaystyle \left\{\begin{align}
r^2 &= \sqrt{2}\,,\\[5pt] 2\alpha &= \frac{\pi}{4}+2n\pi\,,\quad \end{align}\right. |
Dies ergibt
| \displaystyle \left\{\begin{align}
r &= \sqrt{\sqrt{2}} = \bigl(2^{1/2}\bigr)^{1/2} = 2^{1/4} = \sqrt[4]{2}\,,\\[5pt] \alpha &= \frac{\pi}{8}+n\pi\,,\quad \end{align}\right. |
Dies entspricht zwei Lösungen, nachdem alle geraden Zahlen dem Argument \displaystyle \pi/8 entsprechen, plus ein Multipel von \displaystyle 2\pi, und alle ungerade Zahlen dem Argument \displaystyle 9\pi/8 entsprechen, plus ein Multipel von \displaystyle 2\pi.
In Polarform lauten die Lösungen also
| \displaystyle z = \left\{\begin{align}
&\sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8}\Bigr)\,,\\[5pt] &\sqrt[4]{2}\Bigl(\cos\frac{9\pi}{8} + i\sin\frac{9\pi}{8}\Bigr)\,\textrm{.} \end{align}\right. |
Eine Lösung, \displaystyle z=\sqrt[4]{2}(\cos (\pi/8) + i\sin (\pi/8) liegt im ersten Quadrant und die zweite Lösung, \displaystyle z=\sqrt[4]{2}(\cos (9\pi/8) + i\sin (9\pi/8)) liegt im dritten Quadrant.
Auf der Form a + bi
Wir schreiben hier \displaystyle z=x+iy und versuchen die Konstanten \displaystyle x und \displaystyle y zu bestimmen.
Mit \displaystyle z=x+iy, erhalten wir die Gleichung
| \displaystyle \begin{align}
(x+iy)^2 &= 1+i\,,\\[5pt] x^2-y^2+2xyi &= 1+i\,\textrm{.} \end{align} |
Nachdem der Real- und Imaginärteil der beiden Seiten gleich sein muss, erhalten wir
| \displaystyle \left\{\begin{align}
x^2 - y^2 &= 1\,,\\[5pt] 2xy &= 1\,\textrm{.} \end{align}\right. |
Wir können hier \displaystyle x und \displaystyle y direkt bestimmen, aber um es einfacher zu machen, berechnen wir den Betrag von beiden Seiten,
| \displaystyle x^2 + y^2 = \sqrt{1^2+1^2} = \sqrt{2}\,\textrm{.} |
und wir erhalten insgesamt dre Gleihungen,
| \displaystyle \left\{\begin{align}
x^2 -y^2 &= 1\,,\\[5pt] 2xy &= 1\,,\\[5pt] x^2 + y^2 &= \sqrt{2}\,\textrm{.} \end{align}\right. |
Addieren wir die erste Gleichung zur dritten erhalten wir
| \displaystyle x^2 | \displaystyle {}-{} | \displaystyle y^2 | \displaystyle {}={} | \displaystyle 1 | |
| \displaystyle +\ \ | \displaystyle x^2 | \displaystyle {}+{} | \displaystyle y^2 | \displaystyle {}={} | \displaystyle \sqrt{2} |
| \displaystyle 2x^2 | \displaystyle {}={} | \displaystyle \sqrt{2}+1 | |||
und wir erhalten,
| \displaystyle x=\pm \sqrt{\frac{\sqrt{2}+1}{2}}\,\textrm{.} |
Subtrahieren wir die erste Gleichung von der dritten erhalten wir,
| \displaystyle x^2 | \displaystyle {}+{} | \displaystyle y^2 | \displaystyle {}={} | \displaystyle \sqrt{2} | |
| \displaystyle -\ \ | \displaystyle \bigl(x^2 | \displaystyle {}-{} | \displaystyle y^2 | \displaystyle {}={} | \displaystyle 1\bigr) |
| \displaystyle 2y^2 | \displaystyle {}={} | \displaystyle \sqrt{2}-1 | |||
und wir erhalten,
| \displaystyle y=\pm \sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.} |
Insgesamt haben wir also vier mögliche Lösungen
| \displaystyle \left\{\begin{align}
x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align} \right. |
Die zweite Gleichung sagt auch, dass \displaystyle xy positiv sein soll, und wir behalten daher nur die Gleichungen
| \displaystyle \left\{\begin{align}
x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \qquad\text{und}\qquad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. |
Nachdem wir wissen, dass unsere Gleichung zwei Lösungen hat, müssen dies unsere Lösungen sein:
| \displaystyle z = \left\{\begin{align}
\sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}\,,\\[5pt] -\sqrt{\frac{\sqrt{2}+1}{2}} - i\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.} \end{align}\right. |
Vergleichen wir diese Lösungen mit den Lösungen in Polarform, erhalten wir
| \displaystyle \sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8} \Bigr) = \sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}} |
und daher ist
| \displaystyle \begin{align}
\cos\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}+1}{2}}\,,\\[5pt] \sin\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.} \end{align} |
und wir erhalten auch
| \displaystyle \tan\frac{\pi}{8} = \frac{\sin\dfrac{\pi}{8}}{\cos\dfrac{\pi}{8}} = \frac{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}-1}{2}}}{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}+1}{2}}} = \sqrt {\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\,\textrm{.} |
Wir können diesen Ausdruck vereinfachen, indem wir den Ausdruck mit den konjugieren Nenner erweitern,
| \displaystyle \begin{align}
\tan\frac{\pi}{8} &= \sqrt {\frac{(\sqrt{2}-1)(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}} = \sqrt {\frac{(\sqrt{2}-1)^2}{(\sqrt{2})^2-1^2}}\\[5pt] &= \sqrt{\frac{(\sqrt{2}-1)^2}{2-1}} = \sqrt{(\sqrt{2}-1)^2} = \sqrt{2}-1\,\textrm{.} \end{align} |