Lösung 3.2:4a

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 3.2:4a moved to Solution 3.2:4a: Robot: moved page)
Aktuelle Version (16:21, 22. Aug. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 5 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
Der Betrag von <math>3+4i</math> ist der Abstand zum Punkt <math>(0,0)</math> in der komplexen Zahlenebene.
-
<center> [[Image:3_2_4a.gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
Durch den Satz des Pythagoras erhalten wir den Abstand
 +
 
 +
{{Abgesetzte Formel||<math>|3+4i| = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5\,\textrm{.}</math>}}
[[Image:3_2_4_a.gif|center]]
[[Image:3_2_4_a.gif|center]]
 +
 +
 +
Hinweis: Allgemein ist der Betrag einer komplexen Zahl <math>z=x+iy</math>,
 +
 +
{{Abgesetzte Formel||<math>|z| = |x+iy| = \sqrt{x^2+y^2}\,\textrm{.}</math>}}

Aktuelle Version

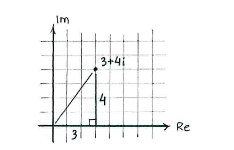
Der Betrag von \displaystyle 3+4i ist der Abstand zum Punkt \displaystyle (0,0) in der komplexen Zahlenebene.

Durch den Satz des Pythagoras erhalten wir den Abstand

\displaystyle |3+4i| = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5\,\textrm{.}


Hinweis: Allgemein ist der Betrag einer komplexen Zahl \displaystyle z=x+iy,

\displaystyle |z| = |x+iy| = \sqrt{x^2+y^2}\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:4a“