Lösung 3.2:2b

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Aktuelle Version (16:00, 22. Aug. 2009) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 4 dazwischen liegende Versionen mit ein.)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
Wir können die Ungleichung <math> 0\leq \mathop{\rm Re} z \leq \mathop{\rm Im} z \leq 1</math> in mehrere Ungleichungen aufteilen:
-
The inequality <math>0\leq \mathrm{Re}z \leq \mathrm{Im}z \leq 1</math> is actually several inequalities:
+
-
<math>\begin{align}
+
:*<math>0 \leq \mathop{\rm Re} z \leq 1\,</math>,
-
0 &\leq \mathrm{Re}z \leq 1,\\
+
:*<math>0 \leq \mathop{\rm Im}z \leq 1\,</math>,
-
0 &\leq \mathrm{Im}z \leq 1,\end{align}
+
:*<math>\mathop{\rm Re}z \leq \mathop{\rm Im}z\,\textrm{.}</math>
-
\mathrm{Re}z \leq \mathrm{Im}z.
+
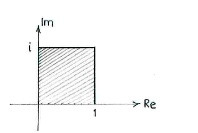
Die ersten zwei Ungleichungen bilden ein Einheitsquadrat in der komplexen Zahlenebene.
-
</math>
+
-
 
+
-
The first two inequalities in this list define the unit square in the complex number plane.
+
[[Image:3_2_2_b1.gif|center]]
[[Image:3_2_2_b1.gif|center]]
-
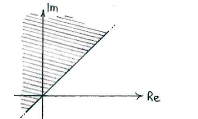
The last inequality says that the real part of <math>z</math> should be less than or equal to the imaginary part of <math>z</math>, I.e. <math>z</math> should lie to the left of the line <math>y=x</math> if <math>x=\mathrm{Re} z</math> and <math>y = \mathrm{Im} z</math>.
+
Die letzte Ungleichung bedeutet, dass der Realteil von <math>z</math> gleich oder geringer als der Imaginärteil von <math>z</math> sein soll. Also muss <math>z</math> links von der Gerade <math>y=x</math> liegen, wo <math>x=\mathop{\rm Re} z</math> und <math>y = \mathop{\rm Im} z</math>.
[[Image:3_2_2_b2.gif|center]]
[[Image:3_2_2_b2.gif|center]]
-
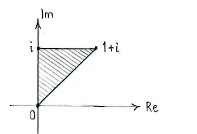
All together, the inequalities define the region which the unit square and the half-plane have in common: a triangle with corner points at <math>0</math>, <math>i</math> and <math>1+i</math>.
+
Zusammen definieren die Ungleichungen ein Dreieck mit den Eckpunkten <math>0</math>, <math>i</math> und <math>1+i</math>.
[[Image:3_2_2_b3.gif|center]]
[[Image:3_2_2_b3.gif|center]]
-
 
-
{{NAVCONTENT_STOP}}
 

Aktuelle Version

Wir können die Ungleichung \displaystyle 0\leq \mathop{\rm Re} z \leq \mathop{\rm Im} z \leq 1 in mehrere Ungleichungen aufteilen:

  • \displaystyle 0 \leq \mathop{\rm Re} z \leq 1\,,
  • \displaystyle 0 \leq \mathop{\rm Im}z \leq 1\,,
  • \displaystyle \mathop{\rm Re}z \leq \mathop{\rm Im}z\,\textrm{.}

Die ersten zwei Ungleichungen bilden ein Einheitsquadrat in der komplexen Zahlenebene.

Die letzte Ungleichung bedeutet, dass der Realteil von \displaystyle z gleich oder geringer als der Imaginärteil von \displaystyle z sein soll. Also muss \displaystyle z links von der Gerade \displaystyle y=x liegen, wo \displaystyle x=\mathop{\rm Re} z und \displaystyle y = \mathop{\rm Im} z.

Zusammen definieren die Ungleichungen ein Dreieck mit den Eckpunkten \displaystyle 0, \displaystyle i und \displaystyle 1+i.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:2b“