Lösung 2.1:1a

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Aktuelle Version (07:25, 21. Aug. 2009) (bearbeiten) (rückgängig)
 
Zeile 1: Zeile 1:
-
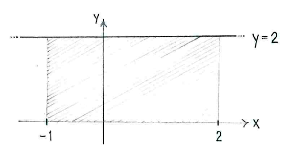
Das Integral entspricht der Fläche unter der Funktion <math>y=2</math> zwischen <math>x=-1\ </math> und <math>x=2</math>.
+
Das Integral entspricht der Fläche unter der Funktion <math>y=2</math> zwischen <math>x=-1 </math> und <math>x=2</math>.
[[Image:2_1_1_a.gif|center]]
[[Image:2_1_1_a.gif|center]]
-
Nachdem diese Fläche ein Rechteck ist, können wir sie leicht berechnen,
+
Da diese Fläche ein Rechteck ist, können wir sie leicht berechnen.
-
{{Abgesetzte Formel||<math>\int\limits_{-1}^{2} 2\,dx = \text{(Basis)}\cdot\text{(Höhe)} = 3\cdot 2 = 6\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>\int\limits_{-1}^{2} 2\,dx = \text{(Basis)}\cdot\text{(Höhe)} = 3\cdot 2 = 6\,\textrm{}</math>}}

Aktuelle Version

Das Integral entspricht der Fläche unter der Funktion \displaystyle y=2 zwischen \displaystyle x=-1 und \displaystyle x=2.

Da diese Fläche ein Rechteck ist, können wir sie leicht berechnen.

\displaystyle \int\limits_{-1}^{2} 2\,dx = \text{(Basis)}\cdot\text{(Höhe)} = 3\cdot 2 = 6\,\textrm{}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:1a“