Lösung 3.3:6

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Solution 3.3:6 moved to Lösung 3.3:6: Robot: moved page)
Zeile 1: Zeile 1:
-
We take up the exercise's challenge and solve the equation both in polar form and in the form <math>a+ib</math>.
 
- 
- 
'''Polar form'''
'''Polar form'''
-
In polar form,
+
Wir lösen die Gleichung zuerst in Polarform,
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 11: Zeile 8:
\end{align}</math>}}
\end{align}</math>}}
-
and, using de Moivre's formula, the equation becomes
+
und durch den Moivrischen Satz erhalten wir die Gleichung
{{Abgesetzte Formel||<math>r^2(\cos 2\alpha + i\sin 2\alpha) = \sqrt{2}\Bigl(\cos \frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>r^2(\cos 2\alpha + i\sin 2\alpha) = \sqrt{2}\Bigl(\cos \frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,\textrm{.}</math>}}
-
If both sides are to be equal, their magnitudes must be equal and their arguments must be equal, other than for multiples of <math>2\pi</math>,
+
Damit die beiden Seiten gleich sein sollen. müssen die Beträge der beiden Seiten gleich sein und die Argumente der beiden Seiten dürfen sich nur mit einen Multipel von <math>2\pi</math> unterscheiden,
{{Abgesetzte Formel||<math>\left\{\begin{align}
{{Abgesetzte Formel||<math>\left\{\begin{align}
Zeile 22: Zeile 19:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
This gives
+
Dies ergibt
{{Abgesetzte Formel||<math>\left\{\begin{align}
{{Abgesetzte Formel||<math>\left\{\begin{align}
Zeile 29: Zeile 26:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
which corresponds two solutions, because all even values of <math>n</math> give the argument <math>\pi/8</math>, to within multiples of <math>2\pi</math>, and all odd values of <math>n</math> give the argument <math>9\pi/8</math>, to within a multiple of <math>2\pi</math>.
+
Dies entspricht zwei Lösungen, nachdem alle geraden Zahlen das Argument <math>\pi/8</math> entsprechen, plus einen Multipel von <math>2\pi</math>, und alle ungerade Zahlen das Argument <math>9\pi/8</math> entsprechen, plus einen Multipel von <math>2\pi</math>.
-
Thus, in polar form, we have the solutions,
+
In Polarform lauten die Lösungen also
{{Abgesetzte Formel||<math>z = \left\{\begin{align}
{{Abgesetzte Formel||<math>z = \left\{\begin{align}
Zeile 38: Zeile 35:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
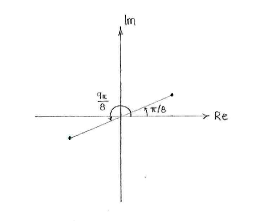
One solution <math>z=\sqrt[4]{2}(\cos (\pi/8) + i\sin (\pi/8)</math> lies in the first quadrant and the second solution <math>z=\sqrt[4]{2}(\cos (9\pi/8) + i\sin (9\pi/8))</math> lies in the third quadrant.
+
 
 +
Eine Lösung, <math>z=\sqrt[4]{2}(\cos (\pi/8) + i\sin (\pi/8)</math> liegt im ersten Quadrant, und die zweite Lösung, <math>z=\sqrt[4]{2}(\cos (9\pi/8) + i\sin (9\pi/8))</math> liegt im dritten Quadrant.
[[Image:3_3_6.gif|center]]
[[Image:3_3_6.gif|center]]
-
'''Rectangular form'''
+
''' Auf der Form ''a'' + ''bi'' '''
-
The alternative way to solve the equation is to put <math>z=x+iy</math> and to try to solve the equation for <math>x</math> and <math>y</math>.
+
Wir schreiben hier <math>z=x+iy</math> und versuchen die Konstanten <math>x</math> und <math>y</math> zu bestimmen.
-
If <math>z=x+iy</math>, the equation becomes
+
Mit <math>z=x+iy</math>, erhalten wir die Gleichung
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 54: Zeile 52:
\end{align}</math>}}
\end{align}</math>}}
-
Because both sides' real and imaginary parts must equal each other we have that
+
Nachdem der Real- und Imaginärteil der beiden Seiten gleich sein muss, erhalten wir
{{Abgesetzte Formel||<math>\left\{\begin{align}
{{Abgesetzte Formel||<math>\left\{\begin{align}
Zeile 61: Zeile 59:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
All the information we need for determining <math>x</math> and <math>y</math> is in these two equations, but it will make things easier if we include an extra relation: the magnitude of both sides should be equal,
+
Wir können hier <math>x</math> und <math>y</math> direkt bestimmen, aber um es einfacher zu machen, berechnen wir den Betrag von beiden Seiten,
{{Abgesetzte Formel||<math>x^2 + y^2 = \sqrt{1^2+1^2} = \sqrt{2}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>x^2 + y^2 = \sqrt{1^2+1^2} = \sqrt{2}\,\textrm{.}</math>}}
-
Therefore, we have in total three equations,
+
und wir erhalten insgesamt dre Gleihungen,
{{Abgesetzte Formel||<math>\left\{\begin{align}
{{Abgesetzte Formel||<math>\left\{\begin{align}
Zeile 73: Zeile 71:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
If we add the first and the third equations,
+
Addieren wir die erste Gleichung zur dritten erhalten wir
{| align="center" style="padding:10px 0px 10px 0px;"
{| align="center" style="padding:10px 0px 10px 0px;"
||
||
Zeile 99: Zeile 97:
|}
|}
-
we get that <math>x</math> must be equal to
+
und wir erhalten;
{{Abgesetzte Formel||<math>x=\pm \sqrt{\frac{\sqrt{2}+1}{2}}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>x=\pm \sqrt{\frac{\sqrt{2}+1}{2}}\,\textrm{.}</math>}}
-
If we subtract the first equation from the third equation,
+
Subtrahieren wir die erste Gleichung von der dritten erhalten wir,
{| align="center" style="padding:10px 0px 10px 0px;"
{| align="center" style="padding:10px 0px 10px 0px;"
||
||
Zeile 129: Zeile 127:
|}
|}
-
we obtain that <math>y</math> must be equal to
+
und wir erhalten;
{{Abgesetzte Formel||<math>y=\pm \sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>y=\pm \sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}</math>}}
-
All in all, this gives us four possible solutions
+
Insgesamt haben wir also vier mögliche Lösungen
{{Abgesetzte Formel||<math>\left\{\begin{align}
{{Abgesetzte Formel||<math>\left\{\begin{align}
Zeile 155: Zeile 153:
\end{align} \right.</math>}}
\end{align} \right.</math>}}
-
although we have only taken account of the first and third equations.
+
Die zweite Gleichung sagt dass <math>xy</math> positiv sein soll, und wir behalten daher nur die Gleichungen
-
 
+
-
The second equation says that the product <math>xy</math> should be positive and then we can directly get rid of solutions in which <math>x</math> and <math>y</math>
+
-
have different signs. Thus, all that is left is
+
{{Abgesetzte Formel||<math>\left\{\begin{align}
{{Abgesetzte Formel||<math>\left\{\begin{align}
Zeile 170: Zeile 165:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
Now, we know already that the equation has two solutions, so we can draw the conclusion that these are
+
Nachdem wir wissen dass unsere Gleichung zwei Lösungen hat, müssen dies unsere Lösungen sein:
{{Abgesetzte Formel||<math>z = \left\{\begin{align}
{{Abgesetzte Formel||<math>z = \left\{\begin{align}
Zeile 177: Zeile 172:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
If we compare the solution in the first quadrant when it is expressed in polar and rectangular forms, we have
+
Vergleichen wir diese Lösungen mit den Lösungen in Polarform, erhalten wir
{{Abgesetzte Formel||<math>\sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8} \Bigr) = \sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}</math>}}
{{Abgesetzte Formel||<math>\sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8} \Bigr) = \sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}</math>}}
-
and therefore we must have that
+
und daher ist
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 188: Zeile 183:
\end{align}</math>}}
\end{align}</math>}}
-
Thus, we have
+
und wir erhalten auch
{{Abgesetzte Formel||<math>\tan\frac{\pi}{8} = \frac{\sin\dfrac{\pi}{8}}{\cos\dfrac{\pi}{8}} = \frac{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}-1}{2}}}{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}+1}{2}}} = \sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\tan\frac{\pi}{8} = \frac{\sin\dfrac{\pi}{8}}{\cos\dfrac{\pi}{8}} = \frac{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}-1}{2}}}{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}+1}{2}}} = \sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\,\textrm{.}</math>}}
-
We can simplify the expression under the square root sign by multiplying top and bottom by the conjugate of the denominator,
+
Wir können diesen Ausdruck vereinfachen, indem wir den Ausdruck mit den konjugieren Nenner erweitern,
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}

Version vom 18:00, 18. Mai 2009

Polar form

Wir lösen die Gleichung zuerst in Polarform,

\displaystyle \begin{align}

z &= r\,(\cos\alpha + i\sin\alpha)\,,\\[5pt] 1+i &= \sqrt{2}\Bigl(\cos\frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,, \end{align}

und durch den Moivrischen Satz erhalten wir die Gleichung

\displaystyle r^2(\cos 2\alpha + i\sin 2\alpha) = \sqrt{2}\Bigl(\cos \frac{\pi}{4} + i\sin\frac{\pi}{4}\Bigr)\,\textrm{.}

Damit die beiden Seiten gleich sein sollen. müssen die Beträge der beiden Seiten gleich sein und die Argumente der beiden Seiten dürfen sich nur mit einen Multipel von \displaystyle 2\pi unterscheiden,

\displaystyle \left\{\begin{align}

r^2 &= \sqrt{2}\,,\\[5pt] 2\alpha &= \frac{\pi}{4}+2n\pi\,,\quad\text{(n is an arbitrary integer).} \end{align}\right.

Dies ergibt

\displaystyle \left\{\begin{align}

r &= \sqrt{\sqrt{2}} = \bigl(2^{1/2}\bigr)^{1/2} = 2^{1/4} = \sqrt[4]{2}\,,\\[5pt] \alpha &= \frac{\pi}{8}+n\pi\,,\quad\text{(n is an arbitrary integer),} \end{align}\right.

Dies entspricht zwei Lösungen, nachdem alle geraden Zahlen das Argument \displaystyle \pi/8 entsprechen, plus einen Multipel von \displaystyle 2\pi, und alle ungerade Zahlen das Argument \displaystyle 9\pi/8 entsprechen, plus einen Multipel von \displaystyle 2\pi.

In Polarform lauten die Lösungen also

\displaystyle z = \left\{\begin{align}

&\sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8}\Bigr)\,,\\[5pt] &\sqrt[4]{2}\Bigl(\cos\frac{9\pi}{8} + i\sin\frac{9\pi}{8}\Bigr)\,\textrm{.} \end{align}\right.


Eine Lösung, \displaystyle z=\sqrt[4]{2}(\cos (\pi/8) + i\sin (\pi/8) liegt im ersten Quadrant, und die zweite Lösung, \displaystyle z=\sqrt[4]{2}(\cos (9\pi/8) + i\sin (9\pi/8)) liegt im dritten Quadrant.


Auf der Form a + bi

Wir schreiben hier \displaystyle z=x+iy und versuchen die Konstanten \displaystyle x und \displaystyle y zu bestimmen.

Mit \displaystyle z=x+iy, erhalten wir die Gleichung

\displaystyle \begin{align}

(x+iy)^2 &= 1+i\,,\\[5pt] x^2-y^2+2xyi &= 1+i\,\textrm{.} \end{align}

Nachdem der Real- und Imaginärteil der beiden Seiten gleich sein muss, erhalten wir

\displaystyle \left\{\begin{align}

x^2 - y^2 &= 1\,,\\[5pt] 2xy &= 1\,\textrm{.} \end{align}\right.

Wir können hier \displaystyle x und \displaystyle y direkt bestimmen, aber um es einfacher zu machen, berechnen wir den Betrag von beiden Seiten,

\displaystyle x^2 + y^2 = \sqrt{1^2+1^2} = \sqrt{2}\,\textrm{.}

und wir erhalten insgesamt dre Gleihungen,

\displaystyle \left\{\begin{align}

x^2 -y^2 &= 1\,,\\[5pt] 2xy &= 1\,,\\[5pt] x^2 + y^2 &= \sqrt{2}\,\textrm{.} \end{align}\right.

Addieren wir die erste Gleichung zur dritten erhalten wir

\displaystyle x^2 \displaystyle {}-{} \displaystyle y^2 \displaystyle {}={} \displaystyle 1
\displaystyle +\ \ \displaystyle x^2 \displaystyle {}+{} \displaystyle y^2 \displaystyle {}={} \displaystyle \sqrt{2}
\displaystyle 2x^2 \displaystyle {}={} \displaystyle \sqrt{2}+1

und wir erhalten;

\displaystyle x=\pm \sqrt{\frac{\sqrt{2}+1}{2}}\,\textrm{.}

Subtrahieren wir die erste Gleichung von der dritten erhalten wir,

\displaystyle x^2 \displaystyle {}+{} \displaystyle y^2 \displaystyle {}={} \displaystyle \sqrt{2}
\displaystyle -\ \ \displaystyle \bigl(x^2 \displaystyle {}-{} \displaystyle y^2 \displaystyle {}={} \displaystyle 1\bigr)
\displaystyle 2y^2 \displaystyle {}={} \displaystyle \sqrt{2}-1

und wir erhalten;

\displaystyle y=\pm \sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.}

Insgesamt haben wir also vier mögliche Lösungen

\displaystyle \left\{\begin{align}

x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \quad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align} \right.

Die zweite Gleichung sagt dass \displaystyle xy positiv sein soll, und wir behalten daher nur die Gleichungen

\displaystyle \left\{\begin{align}

x &= \sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= \sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right. \qquad\text{and}\qquad \left\{\begin{align} x &= -\sqrt{\frac{\sqrt{2}+1}{2}}\\[5pt] y &= -\sqrt{\frac{\sqrt{2}-1}{2}} \end{align}\right.

Nachdem wir wissen dass unsere Gleichung zwei Lösungen hat, müssen dies unsere Lösungen sein:

\displaystyle z = \left\{\begin{align}

\sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}\,,\\[5pt] -\sqrt{\frac{\sqrt{2}+1}{2}} - i\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.} \end{align}\right.

Vergleichen wir diese Lösungen mit den Lösungen in Polarform, erhalten wir

\displaystyle \sqrt[4]{2}\Bigl(\cos\frac{\pi}{8} + i\sin\frac{\pi}{8} \Bigr) = \sqrt{\frac{\sqrt{2}+1}{2}} + i\sqrt{\frac{\sqrt{2}-1}{2}}

und daher ist

\displaystyle \begin{align}

\cos\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}+1}{2}}\,,\\[5pt] \sin\frac{\pi}{8} &= \frac{1}{\sqrt[4]{2}}\sqrt{\frac{\sqrt{2}-1}{2}}\,\textrm{.} \end{align}

und wir erhalten auch

\displaystyle \tan\frac{\pi}{8} = \frac{\sin\dfrac{\pi}{8}}{\cos\dfrac{\pi}{8}} = \frac{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}-1}{2}}}{\dfrac{1}{\sqrt[4]{2}}\sqrt{\dfrac{\sqrt{2}+1}{2}}} = \sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\,\textrm{.}

Wir können diesen Ausdruck vereinfachen, indem wir den Ausdruck mit den konjugieren Nenner erweitern,

\displaystyle \begin{align}

\tan\frac{\pi}{8} &= \sqrt{\frac{(\sqrt{2}-1)(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}} = \sqrt{\frac{(\sqrt{2}-1)^2}{(\sqrt{2})^2-1^2}}\\[5pt] &= \sqrt{\frac{(\sqrt{2}-1)^2}{2-1}} = \sqrt{(\sqrt{2}-1)^2} = \sqrt{2}-1\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.3:6“