Lösung 3.3:2a

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Solution 3.3:2a moved to Lösung 3.3:2a: Robot: moved page)
Zeile 1: Zeile 1:
-
An equation of the type "<math>z^{n} = \text{a complex number}</math>" is called a binomial equation and these are usually solved by going over to polar form and using de Moivre's formula.
+
Eine Gleichung auf der Form "<math>z^{n} = \text{Eine komplexe Zahl}</math>" löst man indem man alle Zahlen auf Polarform bringt, und den Moivreschen Satz benutzt.
-
We start by writing <math>z</math> and <math>1</math> in polar form
+
Wir bringen zuerst <math>z</math> und <math>1</math> auf Polarform
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 8: Zeile 8:
\end{align}</math>}}
\end{align}</math>}}
-
The equation then becomes
+
und erhalten die Gleichung
{{Abgesetzte Formel||<math>r^4(\cos 4\alpha + i\sin 4\alpha) = 1\,(\cos 0 + i\sin 0)\,,</math>}}
{{Abgesetzte Formel||<math>r^4(\cos 4\alpha + i\sin 4\alpha) = 1\,(\cos 0 + i\sin 0)\,,</math>}}
-
where we have used de Moivre's formula on the left-hand side. In order that both sides are equal, they must have the same magnitude and the same argument to within a multiple of <math>2\pi</math>, i.e.
+
wo wir den Moivreschen Satz auf der linken Seite benutzt haben. Damit dir rechte und die linke Seite gleich sein sollen, msen deren Betrag gleich sein, und deren Argument darf sich nur mit einen Multipel von <math>2\pi</math> unterscheiden,
{{Abgesetzte Formel||<math>\left\{\begin{align}
{{Abgesetzte Formel||<math>\left\{\begin{align}
Zeile 19: Zeile 19:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
This means that
+
Also it
{{Abgesetzte Formel||<math>\left\{\begin{align}
{{Abgesetzte Formel||<math>\left\{\begin{align}
Zeile 26: Zeile 26:
\end{align}\right.</math>}}
\end{align}\right.</math>}}
-
The solutions are thus (in polar form)
+
und die Wurzeln sind:
{{Abgesetzte Formel||<math>z = 1\cdot\Bigl(\cos\frac{n\pi}{2} + i\sin\frac{n\pi}{2}\Bigr)\,,\quad\text{for }n=0,\ \pm 1,\ \pm 2,\ldots</math>}}
{{Abgesetzte Formel||<math>z = 1\cdot\Bigl(\cos\frac{n\pi}{2} + i\sin\frac{n\pi}{2}\Bigr)\,,\quad\text{for }n=0,\ \pm 1,\ \pm 2,\ldots</math>}}
-
but observe that the argument on the right-hand side essentially takes only four different values <math>0</math>, <math>\pi/2</math>, <math>\pi</math> and <math>3\pi/2\,</math>, because other values of <math>n</math> give some of these values plus/minus a multiple of <math>2\pi\,</math>.
+
Wir erhalten aber nur vier unterschiedliche winkeln, nämlich <math>0</math>, <math>\pi/2</math>, <math>\pi</math> und <math>3\pi/2\,</math>, nachdem jeder anderer Winkel sich nur mit einen Multipel von <math>2\pi\,</math> von diesen Winkeln unterscheidet.
-
The equation's solutions are therefore
+
Die Wurzeln sind daher
{{Abgesetzte Formel||<math>z=\left\{\begin{align}
{{Abgesetzte Formel||<math>z=\left\{\begin{align}
Zeile 49: Zeile 49:
-
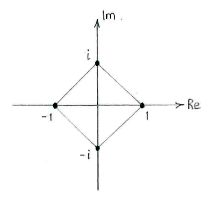
Note: If we mark these solutions on the complex number plane, we see that they are corners in a regular quadrilateral.
 
[[Image:3_3_2_a.gif|center]]
[[Image:3_3_2_a.gif|center]]

Version vom 15:17, 18. Mai 2009

Eine Gleichung auf der Form "\displaystyle z^{n} = \text{Eine komplexe Zahl}" löst man indem man alle Zahlen auf Polarform bringt, und den Moivreschen Satz benutzt.

Wir bringen zuerst \displaystyle z und \displaystyle 1 auf Polarform

\displaystyle \begin{align}

z &= r(\cos\alpha + i\sin\alpha)\,,\\[5pt] 1 &= 1(\cos 0 + i\sin 0)\,\textrm{.} \end{align}

und erhalten die Gleichung

\displaystyle r^4(\cos 4\alpha + i\sin 4\alpha) = 1\,(\cos 0 + i\sin 0)\,,

wo wir den Moivreschen Satz auf der linken Seite benutzt haben. Damit dir rechte und die linke Seite gleich sein sollen, msen deren Betrag gleich sein, und deren Argument darf sich nur mit einen Multipel von \displaystyle 2\pi unterscheiden,

\displaystyle \left\{\begin{align}

r^{4} &= 1\,,\\[5pt] 4\alpha &= 0+2n\pi\,,\quad (\text{n is an arbitrary integer})\,\textrm{.} \end{align}\right.

Also it

\displaystyle \left\{\begin{align}

r &= 1\,,\\[5pt] \alpha &= \frac{n\pi}{2}\,,\quad \text{(n is an arbitrary integer).} \end{align}\right.

und die Wurzeln sind:

\displaystyle z = 1\cdot\Bigl(\cos\frac{n\pi}{2} + i\sin\frac{n\pi}{2}\Bigr)\,,\quad\text{for }n=0,\ \pm 1,\ \pm 2,\ldots

Wir erhalten aber nur vier unterschiedliche winkeln, nämlich \displaystyle 0, \displaystyle \pi/2, \displaystyle \pi und \displaystyle 3\pi/2\,, nachdem jeder anderer Winkel sich nur mit einen Multipel von \displaystyle 2\pi\, von diesen Winkeln unterscheidet.

Die Wurzeln sind daher

\displaystyle z=\left\{\begin{align}

&1\cdot(\cos 0 + i\sin 0)\,,\\[5pt] &1\cdot(\cos (\pi/2) + i\sin (\pi/2))\,,\\[5pt] &1\cdot(\cos \pi + i\sin \pi)\,,\\[5pt] &1\cdot(\cos (3\pi/2) + i\sin (3\pi/2))\,, \end{align}\right. = \left\{ \begin{align} 1\,,&\\[5pt] i\,,&\\[5pt] -1\,,&\\[5pt] -i\,\textrm{.}& \end{align}\right.


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.3:2a“