Lösung 3.2:6c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Solution 3.2:6c moved to Lösung 3.2:6c: Robot: moved page)
Zeile 1: Zeile 1:
-
We need to know the number's magnitude and argument, in order to be able to write down its polar form.
+
Wir brauchen nur den Betrag und das Argument um die Zahl auf Polarform zu bringen.
-
We obtain the number's magnitude as its distance to the origin; it is obtained by the distance formula,
+
Den betrag erhalten wir durch die Formel
{{Abgesetzte Formel||<math>|-4-4i| = \sqrt{(-4)^2+(-4)^2} = \sqrt{16+16} = \sqrt{16\cdot 2} = 4\sqrt{2}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>|-4-4i| = \sqrt{(-4)^2+(-4)^2} = \sqrt{16+16} = \sqrt{16\cdot 2} = 4\sqrt{2}\,\textrm{.}</math>}}
-
Furthermore, the number lies in the third quadrant (negative real and imaginary parts) and if we introduce an auxiliary triangle in that quadrant, we can determine the angle that the number makes with the negative real axis. Then, we get the number's argument by adding the angle <math>\pi</math>.
+
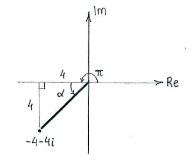
Weiterhin lieht die Zahl in dritten Quadrant, und definieren wir ein Dreieck wie in der Figur, können wir zuerst den Winkel <math>\alpha</math> bestimmen. Addieren wir <math>\pi</math> zu diesen Winkel, erhalten wir das Argument.
<center>[[Image:3_2_6_c1.gif]] [[Image:3_2_6_c2.gif]]</center>
<center>[[Image:3_2_6_c1.gif]] [[Image:3_2_6_c2.gif]]</center>
-
The number's polar form is thus
+
Die Polarform der Zahl ist daher
{{Abgesetzte Formel||<math>4\sqrt{2}\Bigl(\cos\frac{5\pi}{4} + i\sin\frac{5\pi}{4} \Bigr)\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>4\sqrt{2}\Bigl(\cos\frac{5\pi}{4} + i\sin\frac{5\pi}{4} \Bigr)\,\textrm{.}</math>}}

Version vom 13:09, 13. Mai 2009

Wir brauchen nur den Betrag und das Argument um die Zahl auf Polarform zu bringen.

Den betrag erhalten wir durch die Formel

\displaystyle |-4-4i| = \sqrt{(-4)^2+(-4)^2} = \sqrt{16+16} = \sqrt{16\cdot 2} = 4\sqrt{2}\,\textrm{.}

Weiterhin lieht die Zahl in dritten Quadrant, und definieren wir ein Dreieck wie in der Figur, können wir zuerst den Winkel \displaystyle \alpha bestimmen. Addieren wir \displaystyle \pi zu diesen Winkel, erhalten wir das Argument.

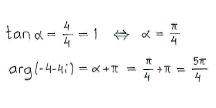
Image:3_2_6_c1.gif Image:3_2_6_c2.gif

Die Polarform der Zahl ist daher

\displaystyle 4\sqrt{2}\Bigl(\cos\frac{5\pi}{4} + i\sin\frac{5\pi}{4} \Bigr)\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:6c“