Lösung 3.2:6a
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
K (Solution 3.2:6a moved to Lösung 3.2:6a: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | Die Polarform ist nur eine Art komplexe Zahlen zu schreiben. Nachdem ein Vektor eindeutig durch seinen Betrag und Argument (Winkel) definiert ist, gilt dasselbe auch für komplexe Zahlen. | |
[[Image:3_2_6_a.gif|center]] | [[Image:3_2_6_a.gif|center]] | ||
| - | + | Anstatt dass wir die komplexe Zahl wie | |
| - | <math>x+iy</math>, | + | <math>x+iy</math> schreiben, schreiben wir sie in Polarform, um unter anderen Multiplikation und Division zu vereinfachen. |
| - | + | Die Polarform wird definiert durch: | |
{{Abgesetzte Formel||<math>x+iy=r(\cos\alpha + i\sin\alpha)\,,</math>}} | {{Abgesetzte Formel||<math>x+iy=r(\cos\alpha + i\sin\alpha)\,,</math>}} | ||
| - | + | wo <math>x</math> und <math>y</math> reelle Zahlen sind, und <math>r</math> und <math>\alpha</math> der Betrag und das Argument sind. Die rechte Seite der Formen benennt man die Polarform einer komplexen Zahl. | |
| - | + | Die Zahl 3 hat den Betrag 3, und das Argument <math>0</math>, nachdem sie auf der reellen Achse liegt. Daher ist | |
{{Abgesetzte Formel||<math>3(\cos 0 + i\sin 0)\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>3(\cos 0 + i\sin 0)\,\textrm{.}</math>}} | ||
Version vom 13:04, 13. Mai 2009
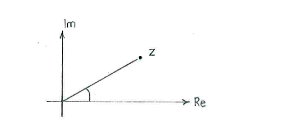
Die Polarform ist nur eine Art komplexe Zahlen zu schreiben. Nachdem ein Vektor eindeutig durch seinen Betrag und Argument (Winkel) definiert ist, gilt dasselbe auch für komplexe Zahlen.
Anstatt dass wir die komplexe Zahl wie \displaystyle x+iy schreiben, schreiben wir sie in Polarform, um unter anderen Multiplikation und Division zu vereinfachen.
Die Polarform wird definiert durch:
| \displaystyle x+iy=r(\cos\alpha + i\sin\alpha)\,, |
wo \displaystyle x und \displaystyle y reelle Zahlen sind, und \displaystyle r und \displaystyle \alpha der Betrag und das Argument sind. Die rechte Seite der Formen benennt man die Polarform einer komplexen Zahl.
Die Zahl 3 hat den Betrag 3, und das Argument \displaystyle 0, nachdem sie auf der reellen Achse liegt. Daher ist
| \displaystyle 3(\cos 0 + i\sin 0)\,\textrm{.} |