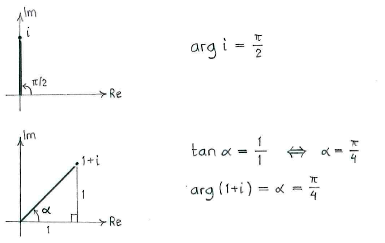Lösung 3.2:5d

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Solution 3.2:5d moved to Lösung 3.2:5d: Robot: moved page)
Zeile 1: Zeile 1:
-
When dividing two complex numbers, the numerator's magnitude is divided by the denominator's magnitude and the numerator's argument is subtracted from the numerator's argument.
+
Wen wir eine komplexe Zahl durch eine andere dividieren, subtrahieren wir das Argument des Nenners vom Argument des Zählers.
-
The argument of the quotient <math>i/(1+i)</math> is therefore
+
Das Argument von <math>i/(1+i)</math> ist daher
{{Abgesetzte Formel||<math>\arg\frac{i}{1+i} = \arg i - \arg (1+i)\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\arg\frac{i}{1+i} = \arg i - \arg (1+i)\,\textrm{.}</math>}}
-
We obtain the argument of <math>i</math> and <math>1+i</math> by drawing the numbers in the complex plane and using a little trigonometry.
+
Die Argumente von <math>i</math> und <math>1+i</math> erhalten wir indem wir die Zahlen in der komplexen Zahlenebene einzeichnen, und ein wenig Trigonometrie verwenden.
[[Image:3_2_5_d.gif|center]]
[[Image:3_2_5_d.gif|center]]
-
Hence, we obtain
+
Daher erhalten wir,
{{Abgesetzte Formel||<math>\arg\frac{i}{1+i} = \arg i - \arg (1+i) = \frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4}\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\arg\frac{i}{1+i} = \arg i - \arg (1+i) = \frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4}\,\textrm{.}</math>}}

Version vom 12:55, 13. Mai 2009

Wen wir eine komplexe Zahl durch eine andere dividieren, subtrahieren wir das Argument des Nenners vom Argument des Zählers.

Das Argument von \displaystyle i/(1+i) ist daher

\displaystyle \arg\frac{i}{1+i} = \arg i - \arg (1+i)\,\textrm{.}

Die Argumente von \displaystyle i und \displaystyle 1+i erhalten wir indem wir die Zahlen in der komplexen Zahlenebene einzeichnen, und ein wenig Trigonometrie verwenden.

Daher erhalten wir,

\displaystyle \arg\frac{i}{1+i} = \arg i - \arg (1+i) = \frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4}\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:5d“