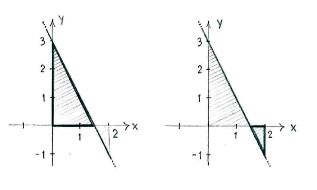Lösung 2.1:1c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Solution 2.1:1c moved to Lösung 2.1:1c: Robot: moved page)
Zeile 1: Zeile 1:
-
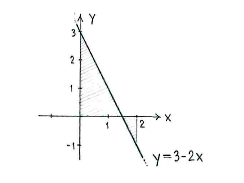
The straight line <math>y=3-2x</math> cuts the ''x''-axis at the point
+
Die Gerade <math>y=3-2x</math> schneidet die ''x''-Achse im Punkt
{{Abgesetzte Formel||<math>y=3-2x=0\quad \Leftrightarrow \quad x=3/2</math>}}
{{Abgesetzte Formel||<math>y=3-2x=0\quad \Leftrightarrow \quad x=3/2</math>}}
-
so the part of the line to the right of <math>x=3/2</math> lies under the ''y''-axis.
+
Also liegt ein Teil der Geraden <math>x=3/2</math> unter der ''y''-Achse.
[[Image:2_1_1_c1.gif|center]]
[[Image:2_1_1_c1.gif|center]]
-
When the curve of a function lies both above and below the ''x''-axis, the value of the integral can be interpreted as “an area having a sign”, which means that, for that part where the curve is under the ''x''-axis, we instead subtract the area between the curve and the ''x''-axis.
+
Wenn wir das Integral berechen, müssen wir berücksichtigen dass die Fläche die unter der ''y''-Achse liegt, von der Fläche oberhalb der ''y''-Achse subtrahiert werden muss.
 +
 
 +
Wir teilen unsere Fläche also auf,
If we divide up the area between the straight line and the ''x''-axis at <math>x=3/2</math>, we see that the value of the integral is the area of the triangle to the left in the figure below, minus the area of the triangle to the right.
If we divide up the area between the straight line and the ''x''-axis at <math>x=3/2</math>, we see that the value of the integral is the area of the triangle to the left in the figure below, minus the area of the triangle to the right.
Zeile 13: Zeile 15:
[[Image:2_1_1_c2.gif|center]]
[[Image:2_1_1_c2.gif|center]]
-
We obtain
+
und erhalten
{{Abgesetzte Formel||<math>\int\limits_{0}^{2} (3-2x)\,dx = \frac{1}{2}\cdot\frac{3}{2}\cdot 3 - \frac{1}{2}\cdot\frac{1}{2}\cdot 1 = \frac{9}{4} - \frac{1}{4} = 2\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\int\limits_{0}^{2} (3-2x)\,dx = \frac{1}{2}\cdot\frac{3}{2}\cdot 3 - \frac{1}{2}\cdot\frac{1}{2}\cdot 1 = \frac{9}{4} - \frac{1}{4} = 2\,\textrm{.}</math>}}

Version vom 15:46, 28. Apr. 2009

Die Gerade \displaystyle y=3-2x schneidet die x-Achse im Punkt

\displaystyle y=3-2x=0\quad \Leftrightarrow \quad x=3/2

Also liegt ein Teil der Geraden \displaystyle x=3/2 unter der y-Achse.

Wenn wir das Integral berechen, müssen wir berücksichtigen dass die Fläche die unter der y-Achse liegt, von der Fläche oberhalb der y-Achse subtrahiert werden muss.

Wir teilen unsere Fläche also auf,

If we divide up the area between the straight line and the x-axis at \displaystyle x=3/2, we see that the value of the integral is the area of the triangle to the left in the figure below, minus the area of the triangle to the right.

und erhalten

\displaystyle \int\limits_{0}^{2} (3-2x)\,dx = \frac{1}{2}\cdot\frac{3}{2}\cdot 3 - \frac{1}{2}\cdot\frac{1}{2}\cdot 1 = \frac{9}{4} - \frac{1}{4} = 2\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:1c“