Lösung 1.3:7

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Solution 1.3:7 moved to Lösung 1.3:7: Robot: moved page)
Zeile 1: Zeile 1:
-
The whole procedure can be illustrated by the figure below:
+
Das Verfahren wird hier deutlich illustriert:
[[Image:1_3_7_1_1.gif|center]]
[[Image:1_3_7_1_1.gif|center]]
-
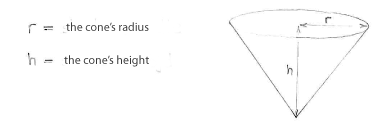
Because it is the cornet's volume we want to maximise, it is appropriate to start by introducing some notation for the dimensions of the cornet.
+
Nachdem wir den Volumen des Kegels maximieren wollen, definieren wir die Maße des Kegels.
[[Image:1_3_7_1_2.gif|center]]
[[Image:1_3_7_1_2.gif|center]]
-
With these dimensions, the volume of the cornet will be the same as that of a cone,
+
Mit diesen Maßen wird der Volumen des Kegels,
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
-
V &= \frac{1}{3}\text{(area of upper circle)}\cdot\text{(height)}\\[5pt]
+
V &= \frac{1}{3}\text{(Fläche des Kreises)}\cdot\text{(Höhe)}\\[5pt]
&= \frac{1}{3}\pi r^{2}h\,\textrm{.}
&= \frac{1}{3}\pi r^{2}h\,\textrm{.}
\end{align}</math>}}
\end{align}</math>}}
-
To go further, we now need to express the radius <math>r</math> and the height <math>h</math> in terms of the angle <math>\alpha</math> on the removed circular sector, so that we can seek the maximum of the volume <math>V</math> when <math>\alpha </math> varies.
+
Wir müssen jetzt den Radius <math>r</math> und die Höhe <math>h</math> durch den Winkel <math>\alpha</math> schreiben, sodass wir den Volumen <math>V</math> als Funktion von <math>\alpha </math> schreiben können.
-
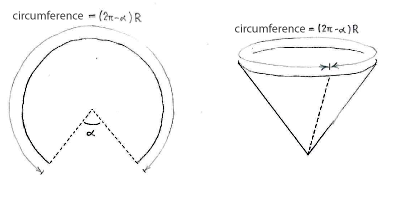
When we cut out a circular sector of angle <math>\alpha</math> from a circular disk, the remaining part of the circular disc's periphery will have length
+
Schneiden wir einen Kreissektor mit dem Winkel <math>\alpha</math> von den Kreis weg, wird der Radius des über gebliebenen Kreises
-
<math>(2\pi-\alpha)R</math>, where <math>R</math> is the radius of the circular disc. This periphery will then become the cornet's upper circular edge, which therefore has the same circumference.
+
<math>(2\pi-\alpha)R</math> sein, wo <math>R</math> der ursprüngliche Radius ist.
[[Image:1_3_7_1_3.gif|center]]
[[Image:1_3_7_1_3.gif|center]]
-
On the other hand, the cornet's upper circular edge has a circumference
+
Der Umfang des oberen Kreises ist aber auch
-
<math>2\pi r</math>, so we must therefore have the relation
+
<math>2\pi r</math>, und also haben wir
{{Abgesetzte Formel||<math>2\pi r = (2\pi-\alpha)R\quad\Leftrightarrow\quad r = \frac{2\pi -\alpha}{2\pi}\,R\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>2\pi r = (2\pi-\alpha)R\quad\Leftrightarrow\quad r = \frac{2\pi -\alpha}{2\pi}\,R\,\textrm{.}</math>}}
-
We have thus managed to express the radius <math>r</math> in terms of the angle
+
Jetzt haben wir also den neuen Radius <math>r</math> als Funktion von den Winkel
-
<math>\alpha</math> (and the radius <math>R</math> of the original circle).
+
<math>\alpha</math> und den ursprünglichen Radius <math>R</math> geschrieben.
-
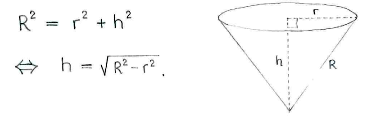
In order to obtain the height <math>h</math>, we can use the fact that we know that the distance from the cornet's tip to its upper edge is equal to the radius <math>R</math> of the original circle. Pythagoras' theorem now gives
+
Um die Höhe zu beschreiben, benutzen wir das Gesetz des Pythagoras
[[Image:1_3_7_1_4.gif||center]]
[[Image:1_3_7_1_4.gif||center]]
-
This means that
+
Also haben wir
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 41: Zeile 41:
\end{align}</math>}}
\end{align}</math>}}
-
Hence, we have expressed <math>r</math> and <math>h</math> in terms of the angle
+
Jetzt haben wir den Radius <math>r</math> und die Höhe <math>h</math> als Funktionen von
-
<math>\alpha</math> and the radius <math>R</math>, and we get that the volume of the cornet is given by
+
<math>\alpha</math> und <math>R</math>, geschrieben. Der Volumen des Kegels ist also
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 50: Zeile 50:
\end{align}</math>}}
\end{align}</math>}}
-
At last, we can mathematically formulate the problem:
+
Unser Problem ist jetzt:
-
::Maximise <math>V(\alpha) = \frac{1}{3}\pi R^3 \Bigl(\frac{2\pi-\alpha}{2\pi} \Bigr)^2\sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,</math>, where <math>0\le \alpha \le 2\pi\,</math>.
+
::Maximiere <math>V(\alpha) = \frac{1}{3}\pi R^3 \Bigl(\frac{2\pi-\alpha}{2\pi} \Bigr)^2\sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,</math>, wo <math>0\le \alpha \le 2\pi\,</math>.
-
Before we start to try and solve this problem, we can observe that the variable
+
Bevor wir anfangen die Funktion abzuleiten, sehen wir dass dar Winkel
-
<math>\alpha</math> occurs in the volume function only in the combination
+
<math>\alpha</math> nur in
-
<math>(2\pi-\alpha)/2\pi</math>, so that we may as well choose to maximise the volume with respect to the variable <math>x=(2\pi-\alpha)/2\pi</math> to obtain, as far as the formula is concerned, the somewhat easier problem:
+
<math>(2\pi-\alpha)/2\pi</math>-Termen auftritt, und also können wir den Volumen genauso in Bezug auf den Variabel <math>x=(2\pi-\alpha)/2\pi</math> maximieren, um das Problem zu vereinfachen,
-
::Maximise <math>V(x) = \frac{1}{3}\pi R^3x^2\sqrt{1-x^2}\,</math>, when <math>0\le x\le 1\,</math>.
+
::Maximiere <math>V(x) = \frac{1}{3}\pi R^3x^2\sqrt{1-x^2}\,</math>, wenn <math>0\le x\le 1\,</math>.
-
When either <math>x=0</math> or <math>x=1</math>, the volume is zero and since the volume function is a differentiable function of <math>x</math> (apart from at <math>x=1</math>), the volume must be a maximum at a critical point of the function.
+
Wenn <math>x=0</math> oder <math>x=1</math>, ist der Volumen null, und nachdem die Funktion überall außer in <math>x=1</math> ableitbar ist, nimmt der Volumen sein Maxima an einen stationären Punkt an.
-
We differentiate,
+
Wir leiten die Funktion ab,
{{Abgesetzte Formel||<math>V'(x) = \frac{1}{3}\pi R^3\cdot 2x\cdot \sqrt{1-x^2} + \frac{1}{3}\pi R^3x^2\cdot\frac{1}{2\sqrt{1-x^2}}\cdot (-2x)\,,</math>}}
{{Abgesetzte Formel||<math>V'(x) = \frac{1}{3}\pi R^3\cdot 2x\cdot \sqrt{1-x^2} + \frac{1}{3}\pi R^3x^2\cdot\frac{1}{2\sqrt{1-x^2}}\cdot (-2x)\,,</math>}}
-
and begin simplifying this expression. The strategy is to try to take out as many factors as possible, so that we see more easily when some factor, and hence the derivative, becomes zero,
+
und vereinfachen den Ausdruck, indem wir so viele Faktoren wir möglich herausziehen,
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 74: Zeile 74:
\end{align}</math>}}
\end{align}</math>}}
-
The derivative is zero when <math>x=0</math> (which is an endpoint) or when <math>2-3x^2=0</math>, i.e. <math>x=\sqrt{2/3}\,</math>. (The point <math>x=-\sqrt{2/3}</math> lies outside <math>0\le x\le 1</math>.)
+
Die Ableitung ist null wenn <math>x=0</math> (dies ist auch ein Endpunkt) oder wenn <math>2-3x^2=0</math>, also wenn <math>x=\sqrt{2/3}\,</math>. (Der Punkt <math>x=-\sqrt{2/3}</math> liegt außerhalb des Gebietes <math>0\le x\le 1</math>.)
-
 
+
-
With the help of a table of the sign of the factors,
+
 +
Durch einer Vorzeichentabelle erhalten wir die Vorzeichen der Faktoren,
{| border="1" cellpadding="5" cellspacing="0" align="center"
{| border="1" cellpadding="5" cellspacing="0" align="center"
Zeile 111: Zeile 110:
-
we can write down a table of the sign of the derivative itself,
+
und erhalten dadurch das Vorzeichen der Ableitung selbst
Zeile 138: Zeile 137:
|}
|}
-
 
+
Wir sehen hier dass <math>x=\sqrt{2/3}</math> ein globales Maxima ist. <math>x = \sqrt{2/3}</math> entspricht den Winkel <math>\alpha</math>:
-
and see that <math>x=\sqrt{2/3}</math> is a global maximum. The value <math>x = \sqrt{2/3}</math> corresponds to the <math>\alpha</math>-value
+
{{Abgesetzte Formel||<math>\sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\ \text{radians.}</math>}}
{{Abgesetzte Formel||<math>\sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\ \text{radians.}</math>}}

Version vom 12:45, 27. Apr. 2009

Das Verfahren wird hier deutlich illustriert:

Nachdem wir den Volumen des Kegels maximieren wollen, definieren wir die Maße des Kegels.

Mit diesen Maßen wird der Volumen des Kegels,

\displaystyle \begin{align}

V &= \frac{1}{3}\text{(Fläche des Kreises)}\cdot\text{(Höhe)}\\[5pt] &= \frac{1}{3}\pi r^{2}h\,\textrm{.} \end{align}

Wir müssen jetzt den Radius \displaystyle r und die Höhe \displaystyle h durch den Winkel \displaystyle \alpha schreiben, sodass wir den Volumen \displaystyle V als Funktion von \displaystyle \alpha schreiben können.

Schneiden wir einen Kreissektor mit dem Winkel \displaystyle \alpha von den Kreis weg, wird der Radius des über gebliebenen Kreises \displaystyle (2\pi-\alpha)R sein, wo \displaystyle R der ursprüngliche Radius ist.

Der Umfang des oberen Kreises ist aber auch \displaystyle 2\pi r, und also haben wir

\displaystyle 2\pi r = (2\pi-\alpha)R\quad\Leftrightarrow\quad r = \frac{2\pi -\alpha}{2\pi}\,R\,\textrm{.}

Jetzt haben wir also den neuen Radius \displaystyle r als Funktion von den Winkel \displaystyle \alpha und den ursprünglichen Radius \displaystyle R geschrieben.

Um die Höhe zu beschreiben, benutzen wir das Gesetz des Pythagoras

Also haben wir

\displaystyle \begin{align}

h &= \sqrt{R^2-\Bigl(\frac{2\pi-\alpha}{2\pi}\,R\Bigr)^2}\\[5pt] &= \sqrt{R^2-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2R^2}\\[5pt] &= R\sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,\textrm{.} \end{align}

Jetzt haben wir den Radius \displaystyle r und die Höhe \displaystyle h als Funktionen von \displaystyle \alpha und \displaystyle R, geschrieben. Der Volumen des Kegels ist also

\displaystyle \begin{align}

V &= \frac{1}{3}\pi r^2 h\\[5pt] &= \frac{1}{3}\pi \Bigl(\frac{2\pi-\alpha}{2\pi}R\Bigr)^2 R\sqrt{1-\Bigl( \frac{2\pi-\alpha}{2\pi}\Bigr)^2}\\[5pt] &= \frac{1}{3}\pi R^3\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2 \sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,\textrm{.} \end{align}

Unser Problem ist jetzt:

Maximiere \displaystyle V(\alpha) = \frac{1}{3}\pi R^3 \Bigl(\frac{2\pi-\alpha}{2\pi} \Bigr)^2\sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,, wo \displaystyle 0\le \alpha \le 2\pi\,.

Bevor wir anfangen die Funktion abzuleiten, sehen wir dass dar Winkel \displaystyle \alpha nur in \displaystyle (2\pi-\alpha)/2\pi-Termen auftritt, und also können wir den Volumen genauso in Bezug auf den Variabel \displaystyle x=(2\pi-\alpha)/2\pi maximieren, um das Problem zu vereinfachen,

Maximiere \displaystyle V(x) = \frac{1}{3}\pi R^3x^2\sqrt{1-x^2}\,, wenn \displaystyle 0\le x\le 1\,.

Wenn \displaystyle x=0 oder \displaystyle x=1, ist der Volumen null, und nachdem die Funktion überall außer in \displaystyle x=1 ableitbar ist, nimmt der Volumen sein Maxima an einen stationären Punkt an.

Wir leiten die Funktion ab,

\displaystyle V'(x) = \frac{1}{3}\pi R^3\cdot 2x\cdot \sqrt{1-x^2} + \frac{1}{3}\pi R^3x^2\cdot\frac{1}{2\sqrt{1-x^2}}\cdot (-2x)\,,

und vereinfachen den Ausdruck, indem wir so viele Faktoren wir möglich herausziehen,

\displaystyle \begin{align}

V'(x) &= \frac{2}{3}\pi R^3x\sqrt{1-x^2} - \frac{1}{3}\pi R^3x^3\frac{1}{\sqrt{1-x^2}}\\[5pt] &= \frac{1}{3}\pi R^3\frac{x}{\sqrt{1-x^2}}\bigl[ 2(1-x^2)-x^2\bigr]\\[5pt] &= \frac{1}{3}\pi R^3\frac{x}{\sqrt{1-x^2}}(2-3x^2)\,\textrm{.} \end{align}

Die Ableitung ist null wenn \displaystyle x=0 (dies ist auch ein Endpunkt) oder wenn \displaystyle 2-3x^2=0, also wenn \displaystyle x=\sqrt{2/3}\,. (Der Punkt \displaystyle x=-\sqrt{2/3} liegt außerhalb des Gebietes \displaystyle 0\le x\le 1.)

Durch einer Vorzeichentabelle erhalten wir die Vorzeichen der Faktoren,

\displaystyle x \displaystyle 0 \displaystyle \sqrt{\tfrac{2}{3}} \displaystyle 1
\displaystyle x \displaystyle 0 \displaystyle + \displaystyle + \displaystyle + \displaystyle +
\displaystyle \sqrt{1-x^2} \displaystyle + \displaystyle + \displaystyle + \displaystyle + \displaystyle 0
\displaystyle 2-3x^2 \displaystyle + \displaystyle + \displaystyle 0 \displaystyle - \displaystyle -


und erhalten dadurch das Vorzeichen der Ableitung selbst


\displaystyle x \displaystyle 0 \displaystyle \sqrt{\tfrac{2}{3}} \displaystyle 1
\displaystyle V'(x) \displaystyle 0 \displaystyle + \displaystyle 0 \displaystyle -  
\displaystyle V(x) \displaystyle 0 \displaystyle \nearrow \displaystyle \tfrac{4}{9\sqrt{3}}\pi R^3 \displaystyle \searrow \displaystyle 0

Wir sehen hier dass \displaystyle x=\sqrt{2/3} ein globales Maxima ist. \displaystyle x = \sqrt{2/3} entspricht den Winkel \displaystyle \alpha:

\displaystyle \sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\ \text{radians.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:7“