Lösung 3.2:6c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 3: Zeile 3:
We obtain the number's magnitude as its distance to the origin; it is obtained by the distance formula,
We obtain the number's magnitude as its distance to the origin; it is obtained by the distance formula,
-
{{Displayed math||<math>|-4-4i| = \sqrt{(-4)^2+(-4)^2} = \sqrt{16+16} = \sqrt{16\cdot 2} = 4\sqrt{2}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>|-4-4i| = \sqrt{(-4)^2+(-4)^2} = \sqrt{16+16} = \sqrt{16\cdot 2} = 4\sqrt{2}\,\textrm{.}</math>}}
Furthermore, the number lies in the third quadrant (negative real and imaginary parts) and if we introduce an auxiliary triangle in that quadrant, we can determine the angle that the number makes with the negative real axis. Then, we get the number's argument by adding the angle <math>\pi</math>.
Furthermore, the number lies in the third quadrant (negative real and imaginary parts) and if we introduce an auxiliary triangle in that quadrant, we can determine the angle that the number makes with the negative real axis. Then, we get the number's argument by adding the angle <math>\pi</math>.
Zeile 11: Zeile 11:
The number's polar form is thus
The number's polar form is thus
-
{{Displayed math||<math>4\sqrt{2}\Bigl(\cos\frac{5\pi}{4} + i\sin\frac{5\pi}{4} \Bigr)\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>4\sqrt{2}\Bigl(\cos\frac{5\pi}{4} + i\sin\frac{5\pi}{4} \Bigr)\,\textrm{.}</math>}}

Version vom 13:10, 10. Mär. 2009

We need to know the number's magnitude and argument, in order to be able to write down its polar form.

We obtain the number's magnitude as its distance to the origin; it is obtained by the distance formula,

\displaystyle |-4-4i| = \sqrt{(-4)^2+(-4)^2} = \sqrt{16+16} = \sqrt{16\cdot 2} = 4\sqrt{2}\,\textrm{.}

Furthermore, the number lies in the third quadrant (negative real and imaginary parts) and if we introduce an auxiliary triangle in that quadrant, we can determine the angle that the number makes with the negative real axis. Then, we get the number's argument by adding the angle \displaystyle \pi.

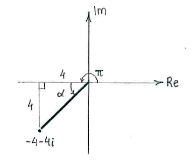
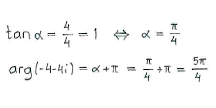
Image:3_2_6_c1.gif Image:3_2_6_c2.gif

The number's polar form is thus

\displaystyle 4\sqrt{2}\Bigl(\cos\frac{5\pi}{4} + i\sin\frac{5\pi}{4} \Bigr)\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:6c“