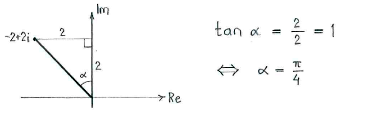Lösung 3.2:5b

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
The number
+
The number <math>-2+2i</math> lies in the second quadrant and if we use an auxiliary triangle in that quadrant (according to the figure), we can use simple trigonometry to determine the angle <math>\alpha</math> which the line between the origin and
-
<math>-\text{2}+\text{2}i</math>
+
<math>-2+2i</math> makes with the positive imaginary axis.
-
lies in the second quadrant and if we use an auxiliary triangle in that quadrant (according to the figure), we can use simple trigonometry to determine the angle <math>\alpha </math> which the line between the origin and
+
-
<math>-\text{2}+\text{2}i</math>
+
-
makes with the positive imaginary axis.
+
-
 
+
[[Image:3_2_5_b1.gif|center]]
[[Image:3_2_5_b1.gif|center]]
-
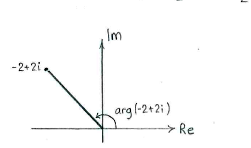
The argument of
+
The argument of <math>-2+2i</math>, which is the angle to the positive real axis, therefore becomes
-
<math>-\text{2}+\text{2}i</math>, which is the angle to the positive real axis, therefore becomes
+
-
 
+
-
 
+
-
<math>\arg \left( -\text{2}+\text{2}i \right)=\frac{\pi }{2}+\alpha =\frac{\pi }{2}+\frac{\pi }{4}=\frac{3\pi }{4}</math>
+
 +
{{Displayed math||<math>\arg (-2+2i) = \frac{\pi}{2} + \alpha = \frac{\pi}{2} + \frac{\pi}{4} = \frac{3\pi}{4}\,\textrm{.}</math>}}
[[Image:3_2_5_b2.gif|center]]
[[Image:3_2_5_b2.gif|center]]

Version vom 12:29, 29. Okt. 2008

The number \displaystyle -2+2i lies in the second quadrant and if we use an auxiliary triangle in that quadrant (according to the figure), we can use simple trigonometry to determine the angle \displaystyle \alpha which the line between the origin and \displaystyle -2+2i makes with the positive imaginary axis.

The argument of \displaystyle -2+2i, which is the angle to the positive real axis, therefore becomes

\displaystyle \arg (-2+2i) = \frac{\pi}{2} + \alpha = \frac{\pi}{2} + \frac{\pi}{4} = \frac{3\pi}{4}\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:5b“