Lösung 3.2:5a

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
The argument of a complex number is angle of the line between the origin and the number measured with respect the positive real number axis.
+
The argument of a complex number is the angle of the line between the origin and the number measured with respect the positive real number axis.
-
 
+
-
In this case, we see directly that
+
-
<math>-\text{1}0</math>
+
-
has the argument
+
-
<math>\pi </math>.
+
 +
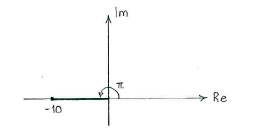
In this case, we see directly that <math>-10</math> has the argument <math>\pi</math>.
[[Image:3_2_5_a.gif|center]]
[[Image:3_2_5_a.gif|center]]
-
NOTE: All angles that correspond to the same direction differ by a whole number of turns, i.e. a multiple of
+
Note: All angles that correspond to the same direction differ by a whole number of turns, i.e. a multiple of <math>2\pi</math>, and therefore we could have just as well answered <math>-\pi</math>, <math>3\pi</math>, <math>5\pi</math> etc. However, it is usual to give the argument between <math>0</math> and <math>2\pi</math> or between <math>-\pi</math> and <math>\pi</math>.
-
<math>2\pi </math>, and therefore we could have just as well answered
+
-
<math>-\pi </math>,
+
-
<math>3\pi </math>,
+
-
<math>5\pi </math>
+
-
etc. However, it is usual to give the argument between
+
-
<math>0</math>
+
-
and
+
-
<math>2\pi </math>
+
-
or between
+
-
<math>-\pi </math>
+
-
and
+
-
<math>\pi </math>.
+

Version vom 12:25, 29. Okt. 2008

The argument of a complex number is the angle of the line between the origin and the number measured with respect the positive real number axis.

In this case, we see directly that \displaystyle -10 has the argument \displaystyle \pi.


Note: All angles that correspond to the same direction differ by a whole number of turns, i.e. a multiple of \displaystyle 2\pi, and therefore we could have just as well answered \displaystyle -\pi, \displaystyle 3\pi, \displaystyle 5\pi etc. However, it is usual to give the argument between \displaystyle 0 and \displaystyle 2\pi or between \displaystyle -\pi and \displaystyle \pi.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:5a“