Lösung 2.1:4e

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
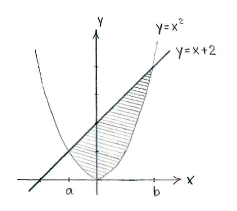
The double inequality means that we look for the area of the region which is bounded above in the y-direction by the straight line
+
The double inequality means that we look for the area of the region which is bounded above in the y-direction by the straight line <math>y=x+2</math> and from below by the parabola <math>y=x^2</math>.
-
<math>y=x+\text{2}</math>
+
-
and from below by the parabola
+
-
<math>y=x^{2}</math>.
+
If we sketch the line and the parabola, the region is given by the region shaded in the figure below.
If we sketch the line and the parabola, the region is given by the region shaded in the figure below.
- 
- 
[[Image:2_1_4_e.gif|center]]
[[Image:2_1_4_e.gif|center]]
 +
As soon as we have determined the ''x''-coordinates of the points of intersection,
 +
<math>x=a</math> and <math>x=b</math>, between the line and the parabola, we can calculate the area as the integral of the difference between the curves' ''y''-values,
-
As soon as we have determined the
+
{{Displayed math||<math>\text{Area} = \int\limits_a^b \bigl(x+2-x^2\bigr)\,dx\,\textrm{.}</math>}}
-
<math>x</math>
+
-
-coordinates of the points of intersection,
+
-
<math>x=a</math>
+
-
and
+
-
<math>x=b</math>, between the line and the parabola, we can calculate the area as the integral of the difference between the curves'
+
-
<math>y</math>
+
-
-values:
+
-
Area=
+
The curves' points of intersection are those points which lie on both curves, i.e. which satisfy both curves' equations
-
<math>\int\limits_{a}^{b}{\left( x+2-x^{2} \right)}\,dx</math>
+
 +
{{Displayed math||<math>\left\{\begin{align}
 +
y &= x+2\,,\\[5pt]
 +
y &= x^2\,\textrm{.}
 +
\end{align} \right.</math>}}
-
The curves' points of intersection are those points which lie on both curves, i.e. which satisfy both curves' equations:
+
By eliminating <math>y</math>, we obtain an equation for <math>x</math>,
-
 
+
-
 
+
-
<math>\left\{ \begin{matrix}
+
-
y=x+\text{2} \\
+
-
y=x^{2} \\
+
-
\end{matrix} \right.</math>
+
-
 
+
-
 
+
-
By eliminating
+
-
<math>y</math>, we obtain an equation for
+
-
<math>x</math>,
+
 +
{{Displayed math||<math>x^{2}=x+2\,\textrm{.}</math>}}
-
<math>x^{2}=x+2</math>
+
If we move all ''x''-terms to the left-hand side,
-
 
+
-
 
+
-
If we move all x-terms to the left-hand side,
+
-
 
+
-
 
+
-
<math>x^{2}-x=2</math>
+
 +
{{Displayed math||<math>x^2-x=2\,,</math>}}
and complete the square, we obtain
and complete the square, we obtain
 +
{{Displayed math||<math>\begin{align}
 +
\Bigl(x-\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 &= 2\\[5pt]
 +
\Bigl(x-\frac{1}{2}\Bigr)^2 &= \frac{9}{4}\,\textrm{.}
 +
\end{align}</math>}}
-
<math>\begin{align}
+
Taking the root then gives that <math>x=\tfrac{1}{2}\pm \tfrac{3}{2}</math>. In other words, <math>x=-1</math> and <math>x=2\,</math>.
-
& \left( x-\frac{1}{2} \right)^{2}-\left( \frac{1}{2} \right)^{2}=2 \\
+
-
& \left( x-\frac{1}{2} \right)^{2}=\frac{9}{4} \\
+
-
\end{align}</math>
+
-
 
+
-
Taking the root then gives that
+
-
<math>x=\frac{1}{2}\pm \frac{3}{2}</math>. In other words,
+
-
<math>x=-\text{1}</math>
+
-
and
+
-
<math>x=\text{2}</math>.
+
The area of the region is now given by
The area of the region is now given by
-
 
+
{{Displayed math||<math>\begin{align}
-
<math>\begin{align}
+
\text{Area}
-
& \text{Area}=\int\limits_{-1}^{2}{\left( x+2-x^{2} \right)}\,dx=\left[ \frac{x^{2}}{2}+2x-\frac{x^{3}}{3} \right]_{-1}^{2} \\
+
&= \int\limits_{-1}^2 \bigl(x+2-x^2\bigr)\,dx\\[5pt]
-
& =\frac{2^{2}}{2}+2\centerdot 2-\frac{2^{3}}{3}-\left( \frac{\left( -1 \right)^{2}}{2}+2\centerdot \left( -1 \right)-\frac{\left( -1 \right)^{3}}{3} \right) \\
+
&= \Bigl[\ \frac{x^2}{2} + 2x - \frac{x^3}{3}\ \Bigr]_{-1}^2\\[5pt]
-
& =2+4-\frac{8}{3}-\frac{1}{2}+2-\frac{1}{3} \\
+
&= \frac{2^2}{2} + 2\cdot 2 - \frac{2^3}{3} - \Bigl( \frac{(-1)^2}{2} + 2\cdot (-1) - \frac{(-1)^3}{3}\Bigr)\\[5pt]
-
& =\frac{9}{2} \\
+
&= 2 + 4 - \frac{8}{3} - \frac{1}{2} + 2 - \frac{1}{3}\\[5pt]
-
\end{align}</math>
+
&= \frac{9}{2}\,\textrm{.}
 +
\end{align}</math>}}

Version vom 09:18, 28. Okt. 2008

The double inequality means that we look for the area of the region which is bounded above in the y-direction by the straight line \displaystyle y=x+2 and from below by the parabola \displaystyle y=x^2.

If we sketch the line and the parabola, the region is given by the region shaded in the figure below.

As soon as we have determined the x-coordinates of the points of intersection, \displaystyle x=a and \displaystyle x=b, between the line and the parabola, we can calculate the area as the integral of the difference between the curves' y-values,

\displaystyle \text{Area} = \int\limits_a^b \bigl(x+2-x^2\bigr)\,dx\,\textrm{.}

The curves' points of intersection are those points which lie on both curves, i.e. which satisfy both curves' equations

\displaystyle \left\{\begin{align}

y &= x+2\,,\\[5pt] y &= x^2\,\textrm{.} \end{align} \right.

By eliminating \displaystyle y, we obtain an equation for \displaystyle x,

\displaystyle x^{2}=x+2\,\textrm{.}

If we move all x-terms to the left-hand side,

\displaystyle x^2-x=2\,,

and complete the square, we obtain

\displaystyle \begin{align}

\Bigl(x-\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 &= 2\\[5pt] \Bigl(x-\frac{1}{2}\Bigr)^2 &= \frac{9}{4}\,\textrm{.} \end{align}

Taking the root then gives that \displaystyle x=\tfrac{1}{2}\pm \tfrac{3}{2}. In other words, \displaystyle x=-1 and \displaystyle x=2\,.

The area of the region is now given by

\displaystyle \begin{align}

\text{Area} &= \int\limits_{-1}^2 \bigl(x+2-x^2\bigr)\,dx\\[5pt] &= \Bigl[\ \frac{x^2}{2} + 2x - \frac{x^3}{3}\ \Bigr]_{-1}^2\\[5pt] &= \frac{2^2}{2} + 2\cdot 2 - \frac{2^3}{3} - \Bigl( \frac{(-1)^2}{2} + 2\cdot (-1) - \frac{(-1)^3}{3}\Bigr)\\[5pt] &= 2 + 4 - \frac{8}{3} - \frac{1}{2} + 2 - \frac{1}{3}\\[5pt] &= \frac{9}{2}\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_2.1:4e“