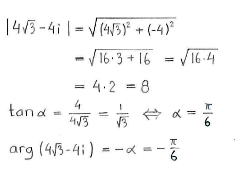Lösung 3.3:1c
Aus Online Mathematik Brückenkurs 2
K (Lösning 3.3:1c moved to Solution 3.3:1c: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | The calculation follows a fairly set pattern. We write the number | |
| - | < | + | <math>4\sqrt{3}-4i</math> |
| - | + | in polar form and then use de Moivre's formula. | |
| + | |||
[[Image:3_3_1_c.gif]] [[Image:3_3_1_c_text.gif]] | [[Image:3_3_1_c.gif]] [[Image:3_3_1_c_text.gif]] | ||
| + | |||
| + | |||
| + | This gives | ||
| + | |||
| + | |||
| + | <math>4\sqrt{3}-4i=8\left( \cos \left( -\frac{\pi }{6} \right)+i\sin \left( -\frac{\pi }{6} \right) \right)</math> | ||
| + | |||
| + | |||
| + | and then we get, on using de Moivre's formula, | ||
| + | |||
| + | |||
| + | <math>\begin{align} | ||
| + | & \left( 4\sqrt{3}-4i \right)^{22}=8^{22}\left( \cos \left( 22\centerdot \left( -\frac{\pi }{6} \right) \right)+i\sin \left( 22\centerdot \left( -\frac{\pi }{6} \right) \right) \right) \\ | ||
| + | & =\left( 2^{3} \right)^{22}\left( \cos \left( -\frac{11\pi }{3} \right)+i\sin \left( -\frac{11\pi }{3} \right) \right) \\ | ||
| + | & =2^{3\centerdot 22}\left( \cos \left( -\frac{12\pi -\pi }{3} \right)+i\sin \left( -\frac{12\pi -\pi }{3} \right) \right) \\ | ||
| + | & =2^{66}\left( \cos \left( -4\pi +\frac{\pi }{3} \right)+i\sin \left( -4\pi +\frac{\pi }{3} \right) \right) \\ | ||
| + | & =2^{66}\left( \cos \left( \frac{\pi }{3} \right)+i\sin \left( \frac{\pi }{3} \right) \right) \\ | ||
| + | & =2^{66}\left( \frac{1}{2}+i\frac{\sqrt{3}}{2} \right)=2^{65}\left( 1+i\sqrt{3} \right) \\ | ||
| + | \end{align}</math> | ||
Version vom 07:28, 24. Okt. 2008
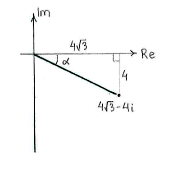
The calculation follows a fairly set pattern. We write the number \displaystyle 4\sqrt{3}-4i in polar form and then use de Moivre's formula.
This gives
\displaystyle 4\sqrt{3}-4i=8\left( \cos \left( -\frac{\pi }{6} \right)+i\sin \left( -\frac{\pi }{6} \right) \right)
and then we get, on using de Moivre's formula,
\displaystyle \begin{align}
& \left( 4\sqrt{3}-4i \right)^{22}=8^{22}\left( \cos \left( 22\centerdot \left( -\frac{\pi }{6} \right) \right)+i\sin \left( 22\centerdot \left( -\frac{\pi }{6} \right) \right) \right) \\
& =\left( 2^{3} \right)^{22}\left( \cos \left( -\frac{11\pi }{3} \right)+i\sin \left( -\frac{11\pi }{3} \right) \right) \\
& =2^{3\centerdot 22}\left( \cos \left( -\frac{12\pi -\pi }{3} \right)+i\sin \left( -\frac{12\pi -\pi }{3} \right) \right) \\
& =2^{66}\left( \cos \left( -4\pi +\frac{\pi }{3} \right)+i\sin \left( -4\pi +\frac{\pi }{3} \right) \right) \\
& =2^{66}\left( \cos \left( \frac{\pi }{3} \right)+i\sin \left( \frac{\pi }{3} \right) \right) \\
& =2^{66}\left( \frac{1}{2}+i\frac{\sqrt{3}}{2} \right)=2^{65}\left( 1+i\sqrt{3} \right) \\
\end{align}