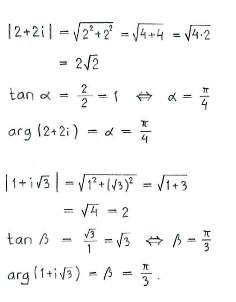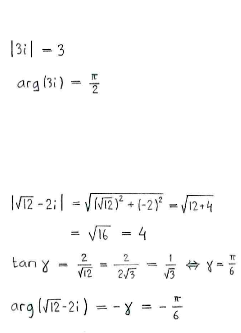Lösung 3.2:6f

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 3.2:6f moved to Solution 3.2:6f: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
We can write every factor in the numerator and denominator in polar form and then use the arithmetical rules for multiplication and division in polar form:
-
<center> [[Image:3_2_6f-1(2).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
 
-
{{NAVCONTENT_START}}
+
<math>\begin{array}{*{35}l}
-
<center> [[Image:3_2_6f-2(2).gif]] </center>
+
\bullet \quad r_{1}\left( \cos \alpha +i\sin \alpha \right)\centerdot r_{2}\left( \cos \beta +i\sin \beta \right)=r_{1}r_{2} \\
-
{{NAVCONTENT_STOP}}
+
\bullet \quad \frac{r_{1}\left( \cos \alpha +i\sin \alpha \right)}{r_{2}\left( \cos \beta +i\sin \beta \right)}=\frac{r_{1}}{r_{2}}\left( \cos \left( \alpha -\beta \right)+i\sin \left( \alpha -\beta \right) \right) \\
 +
\end{array}</math>
 +
 
 +
 
 +
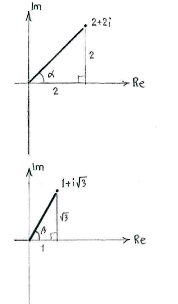
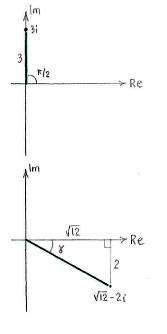
In fact, most of the work consists of writing all the factors in polar form:
 +
 
[[Image:3_2_6_f1_bild.gif]][[Image:3_2_6_f1_bildtext.gif]]
[[Image:3_2_6_f1_bild.gif]][[Image:3_2_6_f1_bildtext.gif]]
[[Image:3_2_6_f2_bild.gif]][[Image:3_2_6_f2_bildtext.gif]]
[[Image:3_2_6_f2_bild.gif]][[Image:3_2_6_f2_bildtext.gif]]
 +
 +
The whole expression becomes
 +
 +
 +
<math>\begin{align}
 +
& \frac{\left( 2+2i \right)\left( 1+i\sqrt{3} \right)}{3i\left( \sqrt{12}-2i \right)}=\frac{2\sqrt{2}\left( \cos \frac{\pi }{4}+i\sin \frac{\pi }{4} \right)\centerdot 2\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right)}{3\left( \cos \frac{\pi }{2}+i\sin \frac{\pi }{2} \right)\centerdot 4\left( \cos \left( -\frac{\pi }{6} \right)+i\sin \left( -\frac{\pi }{6} \right) \right)} \\
 +
& =\frac{4\sqrt{2}\left( \cos \left( \frac{\pi }{4}+\frac{\pi }{3} \right)+i\sin \left( \frac{\pi }{4}+\frac{\pi }{3} \right) \right)}{12\left( \cos \left( \frac{\pi }{2}-\frac{\pi }{6} \right)+i\sin \left( \frac{\pi }{2}-\frac{\pi }{6} \right) \right)} \\
 +
& =\frac{4\sqrt{2}\left( \cos \frac{7\pi }{12}+i\sin \frac{7\pi }{12} \right)}{12\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right)} \\
 +
& =\frac{4\sqrt{2}}{12}\left( \cos \left( \frac{7\pi }{12}-\frac{\pi }{3} \right)+i\sin \left( \frac{7\pi }{12}-\frac{\pi }{3} \right) \right) \\
 +
& =\frac{\sqrt{2}}{3}\left( \cos \frac{\pi }{4}+i\sin \frac{\pi }{4} \right) \\
 +
\end{align}</math>

Version vom 11:00, 23. Okt. 2008

We can write every factor in the numerator and denominator in polar form and then use the arithmetical rules for multiplication and division in polar form:


\displaystyle \begin{array}{*{35}l} \bullet \quad r_{1}\left( \cos \alpha +i\sin \alpha \right)\centerdot r_{2}\left( \cos \beta +i\sin \beta \right)=r_{1}r_{2} \\ \bullet \quad \frac{r_{1}\left( \cos \alpha +i\sin \alpha \right)}{r_{2}\left( \cos \beta +i\sin \beta \right)}=\frac{r_{1}}{r_{2}}\left( \cos \left( \alpha -\beta \right)+i\sin \left( \alpha -\beta \right) \right) \\ \end{array}


In fact, most of the work consists of writing all the factors in polar form:


Image:3_2_6_f1_bild.gifImage:3_2_6_f1_bildtext.gif

Image:3_2_6_f2_bild.gifImage:3_2_6_f2_bildtext.gif

The whole expression becomes


\displaystyle \begin{align} & \frac{\left( 2+2i \right)\left( 1+i\sqrt{3} \right)}{3i\left( \sqrt{12}-2i \right)}=\frac{2\sqrt{2}\left( \cos \frac{\pi }{4}+i\sin \frac{\pi }{4} \right)\centerdot 2\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right)}{3\left( \cos \frac{\pi }{2}+i\sin \frac{\pi }{2} \right)\centerdot 4\left( \cos \left( -\frac{\pi }{6} \right)+i\sin \left( -\frac{\pi }{6} \right) \right)} \\ & =\frac{4\sqrt{2}\left( \cos \left( \frac{\pi }{4}+\frac{\pi }{3} \right)+i\sin \left( \frac{\pi }{4}+\frac{\pi }{3} \right) \right)}{12\left( \cos \left( \frac{\pi }{2}-\frac{\pi }{6} \right)+i\sin \left( \frac{\pi }{2}-\frac{\pi }{6} \right) \right)} \\ & =\frac{4\sqrt{2}\left( \cos \frac{7\pi }{12}+i\sin \frac{7\pi }{12} \right)}{12\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right)} \\ & =\frac{4\sqrt{2}}{12}\left( \cos \left( \frac{7\pi }{12}-\frac{\pi }{3} \right)+i\sin \left( \frac{7\pi }{12}-\frac{\pi }{3} \right) \right) \\ & =\frac{\sqrt{2}}{3}\left( \cos \frac{\pi }{4}+i\sin \frac{\pi }{4} \right) \\ \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:6f“