Lösung 1.3:1d
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
K (Lösning 1.3:1d moved to Solution 1.3:1d: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | The function has critical points at the points | |
| - | < | + | <math>x=a</math> |
| - | + | and | |
| - | + | <math>x=d</math>, (see figure below), i.e. the derivatives are equal to zero, but note that | |
| - | < | + | <math>x=b</math> |
| - | + | and | |
| + | <math>x=c</math> | ||
| + | are not critical points (the derivative is not even defined at these points). | ||
[[Image:1_3_1_d1.gif|center]] | [[Image:1_3_1_d1.gif|center]] | ||
| + | |||
| + | The function has local minimum points at | ||
| + | <math>x=a</math>, | ||
| + | <math>x=c</math> | ||
| + | and the right endpoint of the interval of definition and the local maximum points at the left endpoint, | ||
| + | <math>x=b</math>, and | ||
| + | <math>x=d</math>. Of these, | ||
| + | <math>x=b</math> | ||
| + | is the global maximum and | ||
| + | <math>x=a</math> | ||
| + | is the global minimum. | ||
| + | |||
| + | Between the local extreme points, the function is strictly increasing or decreasing. | ||
| + | |||
| + | |||
[[Image:1_3_1_d2.gif|center]] | [[Image:1_3_1_d2.gif|center]] | ||
Version vom 09:29, 15. Okt. 2008
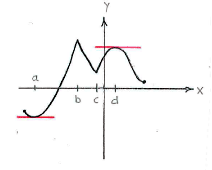
The function has critical points at the points \displaystyle x=a and \displaystyle x=d, (see figure below), i.e. the derivatives are equal to zero, but note that \displaystyle x=b and \displaystyle x=c are not critical points (the derivative is not even defined at these points).
The function has local minimum points at \displaystyle x=a, \displaystyle x=c and the right endpoint of the interval of definition and the local maximum points at the left endpoint, \displaystyle x=b, and \displaystyle x=d. Of these, \displaystyle x=b is the global maximum and \displaystyle x=a is the global minimum.
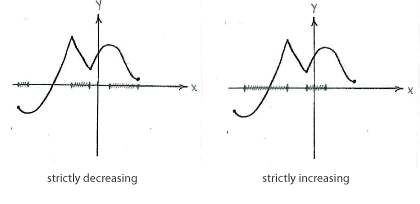
Between the local extreme points, the function is strictly increasing or decreasing.