Aus Online Mathematik Brückenkurs 1

Um die Gleichung \displaystyle \cos 3x = \sin 4x zu lösen, betrachten wir zuerst die allgemeine Gleichung

\displaystyle \cos u=\cos v\,\textrm{.}

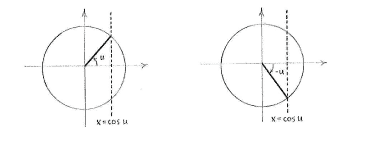
Wir wissen dass es für ein fixes u zwei Winkeln im Einheitskreis gibt für welche die Gleichung erfüllt ist, nämlich \displaystyle v=u und \displaystyle v=-u.

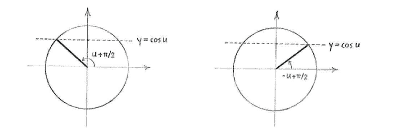
Jetzt drehen wir den Einheitskreis den Winkel \displaystyle \pi/2 gegen den Uhrzeiger. Die Gerade \displaystyle x=\cos u bekommt dann \displaystyle y=\cos u und die Winkeln u und -u bekommen \displaystyle u+\pi/2 und \displaystyle -u+\pi/2,

Die Winkeln \displaystyle u+\pi/2 und \displaystyle -u+\pi/2 haben daher dieselbe y-Koordinate, und daher denselben Sinus. Also ist die Gleichung

\displaystyle \cos u = \sin v

für ein fixes u erfüllt wenn \displaystyle v = \pm u + \pi/2, und allgemein wenn

\displaystyle v = \pm u + \frac{\pi}{2} + 2n\pi\qquad

In unseren Fall ist die Gleichung \displaystyle \cos 3x = \sin 4x erfüllt wenn

\displaystyle 4x = \pm 3x + \frac{\pi}{2} + 2n\pi\,\textrm{.}

und also bekommen wir die allgemeinen Lösungen

\displaystyle \left\{\begin{align} x &= \frac{\pi}{2} + 2n\pi\,,\\[5pt] x &= \frac{\pi}{14} + \frac{2}{7}\pi n\,, \end{align}\right.