Lösung 4.4:7c
Aus Online Mathematik Brückenkurs 1
If we want to solve the equation \displaystyle \text{cos 3}x=\text{sin 4}x, we need an additional result which tells us for which values of \displaystyle u and \displaystyle v the equality \displaystyle \text{cos }u=\text{sin }v holds, but to get that we have to start with the equality \displaystyle \cos u=\cos v.
So, we start by looking at the equality
\displaystyle \cos u=\cos v
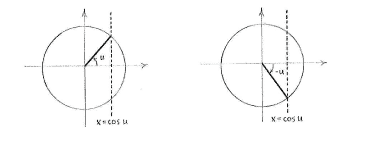
We know that for fixed
\displaystyle u
there are two angles
\displaystyle v=u\text{ }
and
\displaystyle v=-\text{u}
in the unit circle which have the cosine value
\displaystyle \cos u, i.e. their
\displaystyle x
-coordinate is equal to
\displaystyle \cos u.
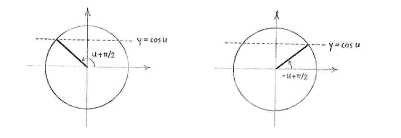
Imagine now that the whole unit circle is rotated anti-clockwise an angle \displaystyle {\pi }/{2}\;. The line \displaystyle x=\cos u will become the line \displaystyle y=\cos u and the angles \displaystyle u and \displaystyle -u are rotated to \displaystyle u+{\pi }/{2}\; and \displaystyle -u+{\pi }/{2}\;, respectively.
The angles \displaystyle u+{\pi }/{2}\; and \displaystyle -u+{\pi }/{2}\; therefore have their \displaystyle y -coordinate, and hence sine value, equal to \displaystyle \cos u. In other words, the equality
\displaystyle \text{cos }u=\text{sin }v
holds for fixed
\displaystyle u
in the unit circle when
\displaystyle v=\pm u+{\pi }/{2}\;, and more generally when
\displaystyle v=\pm u+\frac{\pi }{2}+2n\pi
(
\displaystyle n
an arbitrary integer).
For our equation \displaystyle \text{cos 3}x=\text{sin 4}x, this result means that \displaystyle x\text{ } must satisfy
\displaystyle 4x=\pm 3x+\frac{\pi }{2}+2n\pi
This means that the solutions to the equation are
\displaystyle \left\{ \begin{array}{*{35}l}
x=\frac{\pi }{2}+2n\pi \\
x=\frac{\pi }{14}+\frac{2}{7}\pi n \\
\end{array} \right.
(
\displaystyle n
an arbitrary integer)