Aus Online Mathematik Brückenkurs 1

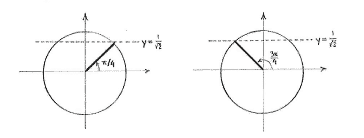
Apart from the fact that there is a \displaystyle \text{5}x, this is a normal trigonometric equation of the type \displaystyle \text{sin }y\text{ }=a . If we are only interested in solutions which satisfy \displaystyle 0\le \text{5}x\le \text{2}\pi , then a sketch of the unit circle shows that there are two such solutions, \displaystyle \text{5}x=\text{ }\frac{\pi }{4} and the reflectionally symmetric solution \displaystyle \text{5}x=\text{ }\pi \text{-}\frac{\pi }{4}=\frac{3\pi }{4}.

All of the equation's solutions are obtained from all values of 5x which differ by a multiple of 2π from either of these two solutions:

\displaystyle \text{5}x=\text{ }\frac{\pi }{4}+2n\pi and \displaystyle \text{5}x=\frac{3\pi }{4}+2n\pi ,

where \displaystyle n is an arbitrary integer.

If we divide both of these by \displaystyle \text{5}, we obtain the solutions expressed in terms of x alone:

\displaystyle x=\frac{\pi }{20}+\frac{2}{5}n\pi and \displaystyle x=\frac{3\pi }{20}+\frac{2}{5}n\pi ,

where \displaystyle n is an arbitrary integer.