Lösung 4.4:7c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 3: Zeile 3:
{{Abgesetzte Formel||<math>\cos u=\cos v\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\cos u=\cos v\,\textrm{.}</math>}}
-
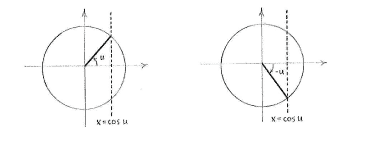
Wir wissen dass es für ein fixes ''u'' zwei Winkeln im Einheitskreis gibt für welche die Gleichung erfüllt ist, nämlich <math>v=u</math> und <math>v=-u</math>.
+
Wir wissen, dass es für ein fixes ''u'' zwei Winkel auf dem Einheitskreis gibt, für welche die Gleichung erfüllt ist, nämlich <math>v=u</math> und <math>v=-u</math>.
[[Image:4_4_7_c1.gif|center]]
[[Image:4_4_7_c1.gif|center]]
-
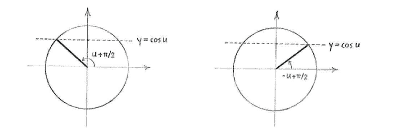
Jetzt drehen wir den Einheitskreis den Winkel <math>\pi/2</math> gegen den Uhrzeiger. Die Gerade <math>x=\cos u</math> bekommt dann <math>y=\cos u</math> und die Winkeln ''u'' und -''u'' bekommen <math>u+\pi/2</math> und <math>-u+\pi/2</math>,
+
Jetzt drehen wir auf dem Einheitskreis den Winkel <math>\pi/2</math> gegen den Uhrzeigersinn. Die Gerade <math>x=\cos u</math> wird dann <math>y=\cos u</math> und die Winkel ''u'' und -''u'' werden <math>u+\pi/2</math> und <math>-u+\pi/2</math>.
[[Image:4_4_7_c2.gif|center]]
[[Image:4_4_7_c2.gif|center]]
-
Die Winkeln <math>u+\pi/2</math> und <math>-u+\pi/2</math> haben daher dieselbe ''y''-Koordinate, und daher denselben Sinus. Also ist die Gleichung
+
Die Winkel <math>u+\pi/2</math> und <math>-u+\pi/2</math> haben daher dieselbe ''y''-Koordinate und daher denselben Sinus. Also ist die Gleichung
{{Abgesetzte Formel||<math>\cos u = \sin v</math>}}
{{Abgesetzte Formel||<math>\cos u = \sin v</math>}}
-
für ein fixes ''u'' erfüllt wenn <math>v = \pm u + \pi/2</math>, und allgemein wenn
+
für ein fixes ''u'' erfüllt, wenn <math>v = \pm u + \pi/2</math>, und allgemein, wenn
-
{{Abgesetzte Formel||<math>v = \pm u + \frac{\pi}{2} + 2n\pi\qquad</math>}}
+
{{Abgesetzte Formel||<math>v = \pm u + \frac{\pi}{2} + 2n\pi\,.</math>}}
-
In unseren Fall ist die Gleichung <math>\cos 3x = \sin 4x</math> erfüllt wenn
+
In unseren Fall ist die Gleichung <math>\cos 3x = \sin 4x</math> erfüllt, wenn
{{Abgesetzte Formel||<math>4x = \pm 3x + \frac{\pi}{2} + 2n\pi\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>4x = \pm 3x + \frac{\pi}{2} + 2n\pi\,\textrm{.}</math>}}
-
und also bekommen wir die allgemeinen Lösungen
+
Also erhalten wir die allgemeinen Lösungen
{{Abgesetzte Formel||<math>\left\{\begin{align}
{{Abgesetzte Formel||<math>\left\{\begin{align}

Version vom 15:01, 19. Jun. 2009

Um die Gleichung \displaystyle \cos 3x = \sin 4x zu lösen, betrachten wir zuerst die allgemeine Gleichung

\displaystyle \cos u=\cos v\,\textrm{.}

Wir wissen, dass es für ein fixes u zwei Winkel auf dem Einheitskreis gibt, für welche die Gleichung erfüllt ist, nämlich \displaystyle v=u und \displaystyle v=-u.

Jetzt drehen wir auf dem Einheitskreis den Winkel \displaystyle \pi/2 gegen den Uhrzeigersinn. Die Gerade \displaystyle x=\cos u wird dann \displaystyle y=\cos u und die Winkel u und -u werden \displaystyle u+\pi/2 und \displaystyle -u+\pi/2.

Die Winkel \displaystyle u+\pi/2 und \displaystyle -u+\pi/2 haben daher dieselbe y-Koordinate und daher denselben Sinus. Also ist die Gleichung

\displaystyle \cos u = \sin v

für ein fixes u erfüllt, wenn \displaystyle v = \pm u + \pi/2, und allgemein, wenn

\displaystyle v = \pm u + \frac{\pi}{2} + 2n\pi\,.

In unseren Fall ist die Gleichung \displaystyle \cos 3x = \sin 4x erfüllt, wenn

\displaystyle 4x = \pm 3x + \frac{\pi}{2} + 2n\pi\,\textrm{.}

Also erhalten wir die allgemeinen Lösungen

\displaystyle \left\{\begin{align}

x &= \frac{\pi}{2} + 2n\pi\,,\\[5pt] x &= \frac{\pi}{14} + \frac{2}{7}\pi n\,, \end{align}\right.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:7c“