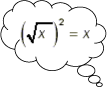3.1 Wurzeln

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
Zeile 62: Zeile 62:
</div>
</div>
-
When taking square roots, it is useful to know some methods of calculation. As <math>\sqrt{a} = a^{1/2}</math> we can use the laws of exponents as "laws of roots". For example, we have
+
Nachdem die Quadratwurzel von a auch wie <math>\sqrt{a} = a^{1/2}</math> geschrieben werden kann, gelten die Rechenregeln für Potenzen auch für Wurzeln. Zum Beispiel haben wir
{{Abgesetzte Formel||<math>\sqrt{9\cdot 4}
{{Abgesetzte Formel||<math>\sqrt{9\cdot 4}
= (9\cdot 4)^{1/2}
= (9\cdot 4)^{1/2}
= 9^{1/2}\cdot 4^{1/2}
= 9^{1/2}\cdot 4^{1/2}
= \sqrt{9}\cdot \sqrt{4}\mbox{.}</math>}}
= \sqrt{9}\cdot \sqrt{4}\mbox{.}</math>}}
-
In this way we obtain the following rules for quadratic roots, which apply to all real numbers <math> a, b \ge 0:</math>
+
In dieser Weise können wir folgende Rechenregeln herleiten, die für alle reellen Zahlen <math> a, b \ge 0:</math> gelten.
<div class="regel">
<div class="regel">
Zeile 76: Zeile 76:
\end{align*}</math>}}
\end{align*}</math>}}
</div>
</div>
-
( We must however, in the above division, assume as always that ''b'' is not 0.)
+
(Bei der Division darf ''b'' natürlich nicht null sein.)
<div class="exempel">
<div class="exempel">
Zeile 95: Zeile 95:
</div>
</div>
-
Note that the above calculations assume that <math>a</math> and <math>b \ge 0</math>. If <math>a</math> and <math>b</math> are negative (<&nbsp;0) then <math>\sqrt{a}</math> and <math>\sqrt{b}</math> are not defined as real numbers. It is tempting to write , for example,
+
Wir müssen beachten dass die Rechenregeln nur gelten wenn <math>a \ge 0</math> und <math>b \ge 0</math>. Wenn <math>a</math> und <math>b</math> beide negativ sind, sind die Wurzeln <math>\sqrt{a}</math> und <math>\sqrt{b}</math> nicht definiert (zumindest nicht als reelle Zahlen). Deshalb kann man zum Beispiel nicht
{{Abgesetzte Formel||<math>-1 = \sqrt{-1} \cdot \sqrt{-1} = \sqrt{ (-1) \cdot (-1) } = \sqrt{1} = 1</math>}}
{{Abgesetzte Formel||<math>-1 = \sqrt{-1} \cdot \sqrt{-1} = \sqrt{ (-1) \cdot (-1) } = \sqrt{1} = 1</math>}}
-
but something here cannot be right. The explanation is that <math> \sqrt{-1} </math> is not a real number, which means the laws of roots discussed above may not be used.
+
schreiben. Dies wein <math> \sqrt{-1} </math> keine reelle Zahl ist, und die Rechenregeln für Wurzeln daher nicht definiert sind.
-
== Higher order roots ==
+
== Allgemeine Wurzeln ==
-
The cube root of a number <math>a</math> is defined as the number that multiplied by itself three times gives <math>a</math>, and is denoted as <math>\sqrt[\scriptstyle 3]{a}</math>.
+
Die Kubikwurzel von <math>a</math> wird durch die Zahl definiert, die mit sich selbst drei Mal multipliziert <math>a</math> ergibt, und wird wie <math>\sqrt[\scriptstyle 3]{a}</math> geschrieben.
<div class="exempel">
<div class="exempel">
Zeile 110: Zeile 110:
<ol type="a">
<ol type="a">
-
<li><math>\sqrt[\scriptstyle 3]{8} = 2 \quad</math> as <math>2
+
<li><math>\sqrt[\scriptstyle 3]{8} = 2 \quad</math> nachdem <math>2
\cdot 2 \cdot 2=8</math>.</li>
\cdot 2 \cdot 2=8</math>.</li>
<li><math>\sqrt[\scriptstyle 3]{0{,}027} = 0{,}3
<li><math>\sqrt[\scriptstyle 3]{0{,}027} = 0{,}3
-
\quad</math> since <math>0{,}3 \cdot 0{,}3 \cdot 0{,}3
+
\quad</math> nachdem <math>0{,}3 \cdot 0{,}3 \cdot 0{,}3
= 0{,}027</math>.</li>
= 0{,}027</math>.</li>
-
<li><math>\sqrt[\scriptstyle 3]{-8} = -2 \quad</math> because <math>(-2)
+
<li><math>\sqrt[\scriptstyle 3]{-8} = -2 \quad</math> nachdem <math>(-2)
\cdot (-2) \cdot (-2)= -8</math>.
\cdot (-2) \cdot (-2)= -8</math>.
</ol>
</ol>
</div>
</div>
-
Note that, unlike square roots, cube roots are also defined for negative numbers.
+
Zum Unterschied von Quadratwurzeln, sind Kubikwurzeln auch für negative Zahlen definiert.
-
For any positive integers <math>n</math> one can define the <math>n</math>'th root of a number <math>a</math> as
+
Für jede Positive Zahl <math>n</math> kann man die <math>n</math>-te Wurzel definieren:
-
* if <math>n</math> is even and <math>a\ge0</math> then <math>\sqrt[\scriptstyle n]{a}</math> is the non-negative number that when multiplied by itself <math>n</math> times gives <math>a</math>,
+
* Wenn <math>n</math> gerade und <math>a\ge0</math> ist, ist <math>\sqrt[\scriptstyle n]{a}</math> die nicht negative Zahl, die hoch <math>n</math> <math>a</math> ergibt,
-
* if <math>n</math> is odd, <math>\sqrt[\scriptstyle n]{a}</math> is the number that when multiplied by itself <math>n</math> times gives <math>a</math>.
+
* Wenn <math>n</math> ungerade ist, ist <math>\sqrt[\scriptstyle n]{a}</math> die Zahl, die hoch <math>n</math> <math>a</math> ergibt,
-
The root <math>\sqrt[\scriptstyle n]{a}</math> can also be written as <math>a^{1/n}</math>.
+
Die Wurzel <math>\sqrt[\scriptstyle n]{a}</math> kann auch wie <math>a^{1/n}</math> geschrieben werden.
<div class="exempel">
<div class="exempel">
Zeile 133: Zeile 133:
<ol type="a">
<ol type="a">
-
<li><math>\sqrt[\scriptstyle 4]{625} = 5\quad</math> since <math>5
+
<li><math>\sqrt[\scriptstyle 4]{625} = 5\quad</math> nachdem <math>5
\cdot 5 \cdot 5 \cdot 5 = 625</math>.</li>
\cdot 5 \cdot 5 \cdot 5 = 625</math>.</li>
-
<li><math>\sqrt[\scriptstyle 5]{-243} = -3\quad</math> because <math>(-3)
+
<li><math>\sqrt[\scriptstyle 5]{-243} = -3\quad</math> nachdem <math>(-3)
\cdot (-3) \cdot (-3) \cdot (-3) \cdot (-3) = -243</math>.</li>
\cdot (-3) \cdot (-3) \cdot (-3) \cdot (-3) = -243</math>.</li>
-
<li><math>\sqrt[\scriptstyle 6]{-17}\quad</math> is not defined as <math>6</math> is even and <math>-17</math> is a negative number. </li>
+
<li><math>\sqrt[\scriptstyle 6]{-17}\quad</math> ist nicht definiert, nachdem <math>6</math> gerade ist, und <math>-17</math> negativ ist. </li>
</ol>
</ol>
</div>
</div>
-
For <math>n</math>'th roots the same rules apply as for quadratic roots if <math>a, \, b \ge 0</math>. Note that if <math>n</math> is odd these methods apply even for negative <math>a</math> and <math>b</math>, that is, for all real numbers <math>a</math> and <math>b</math>.
+
Für die <math>n</math>-te Wurzel gelten dieselben Rechenregeln wir für die Quadratwurzel, falls <math>a, \, b \ge 0</math>. Falls <math>n</math> ungerade ist, gelten die Regeln auch für negative <math>a</math> und <math>b</math>, also für alle reellen Zahlen <math>a</math> und <math>b</math>.
<div class="regel">
<div class="regel">
Zeile 156: Zeile 156:
-
== Simplification of expressions containing roots ==
+
== Vereinfachungen von Wurzelausdrücken ==
-
Often, one can significantly simplify expressions containing roots by using the usual methods for roots . As is also the case when using the laws of exponents, it is desirable to reduce expressions into as "small" roots as possible. For example, it is a good idea to do the following
+
Oft können Ausdrücke die Wurzeln enthalten, wesentlich vereinfacht werden. Generell will man einen Ausdruck mit so kleinen Wurzeln wie möglich erhalten. Zum Beispiel ist die folgende Vereinfachung sinnvoll.
{{Abgesetzte Formel||<math>\sqrt{8}
{{Abgesetzte Formel||<math>\sqrt{8}
Zeile 165: Zeile 165:
= 2\sqrt{2}</math>}}
= 2\sqrt{2}</math>}}
-
because it helps simplification as we see here
+
und ähnlich für die Division,
{{Abgesetzte Formel||<math>\frac{\sqrt{8}}{2}
{{Abgesetzte Formel||<math>\frac{\sqrt{8}}{2}
Zeile 171: Zeile 171:
= \sqrt{2}\mbox{.}</math>}}
= \sqrt{2}\mbox{.}</math>}}
-
By rewriting expressions containing roots in terms of "small" roots one can also sum roots of "the same kind", e.g.
+
Indem man Ausdrücke mit mehreren Termen Term für Term vereinfachen, kann man Terme mit derselben Wurzel addieren.
{{Abgesetzte Formel||<math>\sqrt{8} + \sqrt{2}
{{Abgesetzte Formel||<math>\sqrt{8} + \sqrt{2}
Zeile 233: Zeile 233:
<li><math>(\sqrt{3} + \sqrt{2}\,)(\sqrt{3} - \sqrt{2}\,)
<li><math>(\sqrt{3} + \sqrt{2}\,)(\sqrt{3} - \sqrt{2}\,)
= (\sqrt{3}\,)^2-(\sqrt{2}\,)^2 = 3-2 = 1</math>
= (\sqrt{3}\,)^2-(\sqrt{2}\,)^2 = 3-2 = 1</math>
-
where we have used the difference of two squares <math>(a+b)(a-b) = a^2 - b^2</math> with <math>a=\sqrt{3}</math> and <math>b=\sqrt{2}</math>.</li>
+
Wo wir die binomische Formel <math>(a+b)(a-b) = a^2 - b^2</math> mit <math>a=\sqrt{3}</math> und <math>b=\sqrt{2}</math> benutzt haben.</li>
</ol>
</ol>
</div>
</div>
-
== Rational root expressions ==
+
== Rationale Wurzelausdrücke ==
-
When roots appear in a rational expression one often wants to avoid roots in the denominator (because it is difficult with hand calculations to divide by irrational numbers). By multiplying the numerator and denominator by <math> \sqrt{2} </math> for example, one obtains
+
Wenn man rationale Wurzelausdrücke vereinfacht, will man so weit wie möglich Wurzeln im Nenner vermeiden. Im folgenden Fall können wir den Bruch zum Beispiel mit <math> \sqrt{2} </math> erweitern,
{{Abgesetzte Formel||<math>\frac{1}{\sqrt{2}}
{{Abgesetzte Formel||<math>\frac{1}{\sqrt{2}}
Zeile 246: Zeile 246:
= \frac{\sqrt{2}}{2}</math>}}
= \frac{\sqrt{2}}{2}</math>}}
-
which usually is preferable.
+
Dieser Ausdruck ist viel einfacher zu berechnen oder schätzen, als der vorige.
-
In other cases, you can take advantage of the difference of two squares method, <math>(a+b)(a-b) = a^2 – b^2</math>. One multiplies the numerator and denominator by the denominator´s “conjugate” expression and the root sign is eliminated from the denominator by squaring, as in the following,
+
Wenn der Nenner aus zwei Wurzeln besteht, kann man die binomische formel <math>(a+b)(a-b) = a^2 – b^2</math> benutzen um den Bruch zu vereinfachen. Indem man den Bruch mit den konjugierten Nenner erweitern, erhaltet man immer einen Bruch ohne Wurzeln im Nenner.
{{Abgesetzte Formel||<math>\begin{align*}
{{Abgesetzte Formel||<math>\begin{align*}
Zeile 298: Zeile 298:
'''Diagnostische Prüfung und Schlussprüfung'''
'''Diagnostische Prüfung und Schlussprüfung'''
-
Nachdem Du fertig mit der Theorie bist, sollst Du die diagnostische Prüfung und die Schlussprüfung machen. Du findest die links zu den Prüfungen in Deiner "Student Lounge".
+
Nachdem Sie fertig mit der Theorie sind, sollten Sie die diagnostische Prüfung und die Schlussprüfung machen. Sie finden die links zu den Prüfungen in Ihrer "Student Lounge".
-
'''Bedenke folgendes: '''
+
'''Bedenken Sie folgendes: '''
-
The square root of a number is always non-negative (that is, positive or zero)!
+
Die Quadratwurzel ist immer nicht-negativ, das heißt, positiv oder null.
-
Rules for roots are actually a special case of laws of exponents .
+
Die Rechenregeln für Wurzeln sind nur Spezialfälle der Rechenregeln für Potenzen.
-
For example: <math>\sqrt{x}=x^{1/2}</math>.
+
Zum Beispiel: <math>\sqrt{x}=x^{1/2}</math>.

Version vom 14:31, 23. Mär. 2009

       Theorie          Übungen      

Inhalt:

  • Square roots and n'th roots
  • Manipulating roots

Lernziele:

Nach diesem Abschnitt sollten Sie folgendes können:

  • How to calculate the square root of some simple integers.
  • That the square root of a negative number has not been defined.
  • That the square root of a number denotes the positive root.
  • How to manipulate roots in the simplification of expressions containing roots.
  • To recognise when the methods of manipulating roots are valid. (Non-negative arguments).
  • How to simplify expressions containing quadratic roots in the denominator.
  • When the n'th root of a negative number is defined (n odd).

Quadratwurzeln

Der schon bekannte Symbol \displaystyle \sqrt{a}, bezeichnet die Quadratwurzel einer positiven Zahl \displaystyle a, mit anderen Wörtern die wir bekommen wenn wir a mit a multiplizieren. Es gibt aber eine genauere Definition von der Quadratwurzel.

Der Ausdruck \displaystyle x^2 = 4 hat wie bekannt zwei Wurzeln, \displaystyle x = 2 und \displaystyle x = -2, nachdem \displaystyle 2\cdot 2 = 4 und \displaystyle (-2)\cdot(-2) = 4. Desshalb scheint es natürlich dass \displaystyle \sqrt{4} entweder \displaystyle -2 oder \displaystyle 2, also \displaystyle \sqrt{4}= \pm 2. Dies ist aber nicht der Fall, sondern \displaystyle \sqrt{4} bezeichnet nur die Positive Wurzel \displaystyle 2.


Wie Quadratwurzel \displaystyle \sqrt{a} ist die nicht negative Zahl, die mit sich selbst multipliziert \displaystyle a ergibt, also die nicht negative Lösung der Gleichung \displaystyle x^2 = a.

Die Quadratwurzel von \displaystyle a kann auch wie \displaystyle a^{1/2} geschrieben werden.

Deshalb ist es falsch \displaystyle \sqrt{4}= \pm 2, zu schreiben, aber richtig dass die Gleichung \displaystyle x^2 = 4 die Wurzeln (Lösungen) \displaystyle x = \pm 2 hat.

Beispiel 1

  1. \displaystyle \sqrt{0}=0 \quad nachdem \displaystyle 0^2 = 0 \cdot 0 = 0 und \displaystyle 0 nicht negativ ist.
  2. \displaystyle \sqrt{100}=10 \quad nachdem \displaystyle 10^2 = 10 \cdot 10 = 100 und \displaystyle 10 eine positive Zahl ist.
  3. \displaystyle \sqrt{0{,}25}=0{,}5 \quad nachdem \displaystyle 0{,}5^2 = 0{,}5 \cdot 0{,}5 = 0{,}25 und \displaystyle 0{,}5 eine positive Zahl ist.
  4. \displaystyle \sqrt{2} \approx 1{,}4142 \quad nachdem \displaystyle 1{,}4142 \cdot 1{,}4142 \approx 2 und \displaystyle 1{,}4142 positiv ist.
  5. Die Gleichung \displaystyle x^2=2 hat die Wurzeln (Lösungen) \displaystyle x=\sqrt{2} \approx 1{,}414 und \displaystyle x = -\sqrt{2} \approx -1{,}414.
  6. \displaystyle \sqrt{-4}\quad ist nicht definiert, nachdem es keine reelle Zahl \displaystyle x gibt, die, die Gleichung \displaystyle x^2=-4 erfüllt.
  7. \displaystyle \sqrt{(-7)^2} = 7 \quad nachdem \displaystyle \sqrt{(-7)^2} = \sqrt{(-7) \cdot (-7)} = \sqrt{49} = \sqrt{ 7 \cdot 7} = 7.

Nachdem die Quadratwurzel von a auch wie \displaystyle \sqrt{a} = a^{1/2} geschrieben werden kann, gelten die Rechenregeln für Potenzen auch für Wurzeln. Zum Beispiel haben wir

\displaystyle \sqrt{9\cdot 4} 
 = (9\cdot 4)^{1/2}
 = 9^{1/2}\cdot 4^{1/2}
 = \sqrt{9}\cdot \sqrt{4}\mbox{.}

In dieser Weise können wir folgende Rechenregeln herleiten, die für alle reellen Zahlen \displaystyle a, b \ge 0: gelten.

\displaystyle \begin{align*} 
   \sqrt{ab} &= \sqrt{\vphantom{b}a}\cdot \sqrt{b}\\[4pt]
   \sqrt{\frac{a}{b}} &= \frac{\sqrt{a}}{\sqrt{b}}\\[4pt]
   a\sqrt{b} &= \sqrt{a^2b}
 \end{align*}

(Bei der Division darf b natürlich nicht null sein.)

Beispiel 2

  1. \displaystyle \sqrt{64\cdot 81} = \sqrt{64}\cdot \sqrt{81} = 8\cdot 9 = 72
  2. \displaystyle \sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}
  3. \displaystyle \sqrt{18} \cdot \sqrt{2} = \sqrt{18 \cdot 2} = \sqrt{36} = 6
  4. \displaystyle \frac{\sqrt{75}}{\sqrt{3}} = \sqrt{\frac{75}{3}} = \sqrt{25} = 5
  5. \displaystyle \sqrt{12} = \sqrt{ 4 \cdot 3 } = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}

Wir müssen beachten dass die Rechenregeln nur gelten wenn \displaystyle a \ge 0 und \displaystyle b \ge 0. Wenn \displaystyle a und \displaystyle b beide negativ sind, sind die Wurzeln \displaystyle \sqrt{a} und \displaystyle \sqrt{b} nicht definiert (zumindest nicht als reelle Zahlen). Deshalb kann man zum Beispiel nicht

\displaystyle -1 = \sqrt{-1} \cdot \sqrt{-1} = \sqrt{ (-1) \cdot (-1) } = \sqrt{1} = 1

schreiben. Dies wein \displaystyle \sqrt{-1} keine reelle Zahl ist, und die Rechenregeln für Wurzeln daher nicht definiert sind.


Allgemeine Wurzeln

Die Kubikwurzel von \displaystyle a wird durch die Zahl definiert, die mit sich selbst drei Mal multipliziert \displaystyle a ergibt, und wird wie \displaystyle \sqrt[\scriptstyle 3]{a} geschrieben.

Beispiel 3

  1. \displaystyle \sqrt[\scriptstyle 3]{8} = 2 \quad nachdem \displaystyle 2 \cdot 2 \cdot 2=8.
  2. \displaystyle \sqrt[\scriptstyle 3]{0{,}027} = 0{,}3 \quad nachdem \displaystyle 0{,}3 \cdot 0{,}3 \cdot 0{,}3 = 0{,}027.
  3. \displaystyle \sqrt[\scriptstyle 3]{-8} = -2 \quad nachdem \displaystyle (-2) \cdot (-2) \cdot (-2)= -8.

Zum Unterschied von Quadratwurzeln, sind Kubikwurzeln auch für negative Zahlen definiert.

Für jede Positive Zahl \displaystyle n kann man die \displaystyle n-te Wurzel definieren:

  • Wenn \displaystyle n gerade und \displaystyle a\ge0 ist, ist \displaystyle \sqrt[\scriptstyle n]{a} die nicht negative Zahl, die hoch \displaystyle n \displaystyle a ergibt,
  • Wenn \displaystyle n ungerade ist, ist \displaystyle \sqrt[\scriptstyle n]{a} die Zahl, die hoch \displaystyle n \displaystyle a ergibt,

Die Wurzel \displaystyle \sqrt[\scriptstyle n]{a} kann auch wie \displaystyle a^{1/n} geschrieben werden.

Beispiel 4

  1. \displaystyle \sqrt[\scriptstyle 4]{625} = 5\quad nachdem \displaystyle 5 \cdot 5 \cdot 5 \cdot 5 = 625.
  2. \displaystyle \sqrt[\scriptstyle 5]{-243} = -3\quad nachdem \displaystyle (-3) \cdot (-3) \cdot (-3) \cdot (-3) \cdot (-3) = -243.
  3. \displaystyle \sqrt[\scriptstyle 6]{-17}\quad ist nicht definiert, nachdem \displaystyle 6 gerade ist, und \displaystyle -17 negativ ist.

Für die \displaystyle n-te Wurzel gelten dieselben Rechenregeln wir für die Quadratwurzel, falls \displaystyle a, \, b \ge 0. Falls \displaystyle n ungerade ist, gelten die Regeln auch für negative \displaystyle a und \displaystyle b, also für alle reellen Zahlen \displaystyle a und \displaystyle b.

\displaystyle \begin{align*} 
   \sqrt[\scriptstyle n]{ab}
     &= \sqrt[\scriptstyle n]{\vphantom{b}a}\cdot
          \sqrt[\scriptstyle n]{b}\\[4pt]
   \sqrt[\scriptstyle n]{\frac{a}{b}}
     &= \frac{\sqrt[\scriptstyle n]{a}}{\sqrt[\scriptstyle n]{b}}\\[4pt]
   a\,\sqrt[\scriptstyle n]{b}
     &= \sqrt[\scriptstyle n]{a^nb}
 \end{align*}


Vereinfachungen von Wurzelausdrücken

Oft können Ausdrücke die Wurzeln enthalten, wesentlich vereinfacht werden. Generell will man einen Ausdruck mit so kleinen Wurzeln wie möglich erhalten. Zum Beispiel ist die folgende Vereinfachung sinnvoll.

\displaystyle \sqrt{8} 
 = \sqrt{4\cdot2}
 = \sqrt{4} \cdot \sqrt{2}
 = 2\sqrt{2}

und ähnlich für die Division,

\displaystyle \frac{\sqrt{8}}{2} 
 = \frac{2 \sqrt{2}}{2}
 = \sqrt{2}\mbox{.}

Indem man Ausdrücke mit mehreren Termen Term für Term vereinfachen, kann man Terme mit derselben Wurzel addieren.

\displaystyle \sqrt{8} + \sqrt{2} 
 = 2\sqrt{2} + \sqrt{2}
 = (2+1)\sqrt{2}
 = 3\sqrt{2}\mbox{.}

Beispiel 5

  1. \displaystyle \frac{\sqrt{8}}{\sqrt{18}} = \frac{\sqrt{2 \cdot 4}}{\sqrt{2 \cdot 9}} = \frac{\sqrt{2 \cdot 2 \cdot 2}}{\sqrt{2 \cdot 3 \cdot 3}} = \frac{\sqrt{2 \cdot 2^2}}{\sqrt{2 \cdot 3^2}} = \frac{2\sqrt{2}}{3\sqrt{2}} = \frac{2}{3}
  2. \displaystyle \frac{\sqrt{72}}{6} = \frac{\sqrt{8 \cdot 9}}{ 2 \cdot 3} = \frac{\sqrt{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3}}{ 2 \cdot 3} = \frac{\sqrt{2^2 \cdot 3^2 \cdot 2}}{ 2 \cdot 3} = \frac{2 \cdot 3\sqrt{2}}{2 \cdot 3} = \sqrt{2}
  3. \displaystyle \sqrt{45} + \sqrt{20} = \sqrt{9\cdot5} + \sqrt{4\cdot5} = \sqrt{3^2\cdot5} + \sqrt{2^2\cdot5} = 3\sqrt{5} + 2\sqrt{5}\vphantom{\bigl(}
    \displaystyle \phantom{\sqrt{45} + \sqrt{20}\vphantom{\bigl(}}{} = (3+2)\sqrt{5} = 5\sqrt{5}
  4. \displaystyle \sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(} = \sqrt{5 \cdot 10} + 2\sqrt{3} -\sqrt{2 \cdot 16} + \sqrt{3 \cdot 9}
    \displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{5 \cdot 2 \cdot 5} + 2\sqrt{3} -\sqrt{2 \cdot 4 \cdot 4} + \sqrt{3 \cdot 3 \cdot 3}\vphantom{a^{b^c}}
    \displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{5^2 \cdot 2 } + 2\sqrt{3} -\sqrt{2^2 \cdot 2^2 \cdot 2} + \sqrt{3 \cdot 3^2}\vphantom{a^{\textstyle b^{\textstyle c}}}
    \displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = 5\sqrt{2} +2\sqrt{3} - 2 \cdot 2\sqrt{2} + 3\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}}
    \displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = (5-4)\sqrt{2} + (2+3)\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}}
    \displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{2} + 5\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}}
  5. \displaystyle \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{12} } = \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{3 \cdot 4} } = \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{3} \cdot \sqrt[\scriptstyle3]{4} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{4} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{2 \cdot 2} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{2} \cdot \sqrt[\scriptstyle3]{2} } \cdot \displaystyle \frac{\sqrt[\scriptstyle3]{2}}{ \sqrt[\scriptstyle3]{2}} = \frac{ 2\cdot\sqrt[\scriptstyle3]{2} }{ 2 } = \sqrt[\scriptstyle3]{2}
  6. \displaystyle (\sqrt{3} + \sqrt{2}\,)(\sqrt{3} - \sqrt{2}\,) = (\sqrt{3}\,)^2-(\sqrt{2}\,)^2 = 3-2 = 1 Wo wir die binomische Formel \displaystyle (a+b)(a-b) = a^2 - b^2 mit \displaystyle a=\sqrt{3} und \displaystyle b=\sqrt{2} benutzt haben.


Rationale Wurzelausdrücke

Wenn man rationale Wurzelausdrücke vereinfacht, will man so weit wie möglich Wurzeln im Nenner vermeiden. Im folgenden Fall können wir den Bruch zum Beispiel mit \displaystyle \sqrt{2} erweitern,

\displaystyle \frac{1}{\sqrt{2}} 
 = \frac{1\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}
 = \frac{\sqrt{2}}{2}

Dieser Ausdruck ist viel einfacher zu berechnen oder schätzen, als der vorige.

Wenn der Nenner aus zwei Wurzeln besteht, kann man die binomische formel \displaystyle (a+b)(a-b) = a^2 – b^2 benutzen um den Bruch zu vereinfachen. Indem man den Bruch mit den konjugierten Nenner erweitern, erhaltet man immer einen Bruch ohne Wurzeln im Nenner.

\displaystyle \begin{align*} 
   \frac{\sqrt{3}}{\sqrt{2}+1}
     &= \frac{\sqrt{3}}{\sqrt{2}+1} \cdot \frac{\sqrt{2}-1}{\sqrt{2}-1}
      = \frac{\sqrt{3}\,(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}\\[4pt]
     &= \frac{\sqrt{3}\cdot\sqrt{2} - \sqrt{3}\cdot1}{(\sqrt{2}\,)^2 - 1^2 }
      = \frac{\sqrt{3 \cdot 2} - \sqrt{3}}{ 2 - 1 }
      = \frac{\sqrt{6} - \sqrt{3}}{ 1 }
      = \sqrt{6} - \sqrt{3}\mbox{.}
 \end{align*}

Beispiel 6

  1. \displaystyle \frac{10\sqrt{3}}{\sqrt{5}} = \frac{10\sqrt{3}\cdot\sqrt{5}}{\sqrt{5}\cdot\sqrt{5}} = \frac{10\sqrt{15}}{5} = 2\sqrt{15}
  2. \displaystyle \frac{1+\sqrt{3}}{\sqrt{2}} = \frac{(1+\sqrt{3})\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} = \frac{\sqrt{2}+\sqrt{6}}{2}
  3. \displaystyle \frac{3}{\sqrt{2}-2} = \frac{3(\sqrt{2}+2)}{(\sqrt{2}-2)(\sqrt{2}+2)} = \frac{3\sqrt{2}+6}{(\sqrt{2}\,)^2-2^2} = \frac{3\sqrt{2}+6}{2-4} = -\frac{3\sqrt{2}+6}{2}
  4. \displaystyle \frac{\sqrt{2}}{\sqrt{6}+\sqrt{3}} = \frac{\sqrt{2}\,(\sqrt{6}-\sqrt{3}\,)}{(\sqrt{6}+\sqrt{3}\,) (\sqrt{6}-\sqrt{3}\,)} = \frac{\sqrt{2}\,\sqrt{6}-\sqrt{2}\,\sqrt{3}}{(\sqrt{6}\,)^2 -(\sqrt{3}\,)^2}\vphantom{\Biggl(}
    \displaystyle \phantom{\frac{\sqrt{2}}{\sqrt{6}+\sqrt{3}}\vphantom{\Biggl(}}{} = \frac{\sqrt{2}\,\sqrt{2\cdot 3}-\sqrt{2}\,\sqrt{3}}{6-3} = \frac{2\sqrt{3}-\sqrt{2}\,\sqrt{3}}{3} = \frac{(2-\sqrt{2}\,)\sqrt{3}}{3} \vphantom{\displaystyle\frac{a^{\textstyle b^{\textstyle c}}}{b}}


Übungen


Tipps fürs lernen

Diagnostische Prüfung und Schlussprüfung

Nachdem Sie fertig mit der Theorie sind, sollten Sie die diagnostische Prüfung und die Schlussprüfung machen. Sie finden die links zu den Prüfungen in Ihrer "Student Lounge".

Bedenken Sie folgendes:

Die Quadratwurzel ist immer nicht-negativ, das heißt, positiv oder null.

Die Rechenregeln für Wurzeln sind nur Spezialfälle der Rechenregeln für Potenzen.

Zum Beispiel: \displaystyle \sqrt{x}=x^{1/2}.


Reviews

For those of you who want to deepen your studies or need more detailed explanations consider the following references

Learn more about square roots in the English Wikipedia

How do we know that the root of 2 is not a fraction?


Nützliche Websites

How to find the root of a number, without the help of calculators?

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/3.1_Wurzeln“