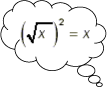3.1 Wurzeln
Aus Online Mathematik Brückenkurs 1
| Zeile 29: | Zeile 29: | ||
[[Image:rotbubbla.gif|right]] | [[Image:rotbubbla.gif|right]] | ||
| - | + | Der schon bekannte Symbol <math>\sqrt{a}</math>, bezeichnet die Quadratwurzel einer positiven Zahl <math>a</math>, mit anderen Wörtern die wir bekommen wenn wir a mit a multiplizieren. Es gibt aber eine genauere Definition von der Quadratwurzel. | |
| - | + | Der Ausdruck <math>x^2 = 4</math> hat wie bekannt zwei Wurzeln, <math>x = 2</math> und <math>x = -2</math>, nachdem <math>2\cdot 2 = 4</math> und <math>(-2)\cdot(-2) = 4</math>. Desshalb scheint es natürlich dass <math>\sqrt{4}</math> entweder <math>-2</math> oder <math>2</math>, also <math>\sqrt{4}= \pm 2</math>. Dies ist aber nicht der Fall, sondern <math>\sqrt{4}</math> bezeichnet nur die Positive Wurzel <math>2</math>. | |
<div class="regel"> | <div class="regel"> | ||
| - | + | Wie Quadratwurzel <math>\sqrt{a}</math> ist die '''nicht negative''' Zahl, die mit sich selbst multipliziert <math>a</math> ergibt, also die nicht negative Lösung der Gleichung <math>x^2 = a</math>. | |
| - | + | ||
| - | + | Die Quadratwurzel von <math>a</math> kann auch wie <math>a^{1/2}</math> geschrieben werden. | |
</div> | </div> | ||
| - | + | Deshalb ist es falsch <math>\sqrt{4}= \pm 2,</math> zu schreiben, aber richtig dass die Gleichung <math>x^2 = 4</math> die Wurzeln (Lösungen) <math>x = \pm 2</math> hat. | |
<div class="exempel"> | <div class="exempel"> | ||
| Zeile 47: | Zeile 46: | ||
<ol type="a"> | <ol type="a"> | ||
| - | <li><math>\sqrt{0}=0 \quad</math> | + | <li><math>\sqrt{0}=0 \quad</math> nachdem <math>0^2 = 0 \cdot 0 |
| - | = 0</math> | + | = 0</math> und <math>0</math> nicht negativ ist. </li> |
| - | <li><math>\sqrt{100}=10 \quad</math> | + | <li><math>\sqrt{100}=10 \quad</math> nachdem <math> 10^2 = 10 \cdot 10 |
| - | = 100 </math> | + | = 100 </math> und <math>10</math> eine positive Zahl ist. </li> |
| - | <li> <math>\sqrt{0{,}25}=0{,}5 \quad</math> | + | <li> <math>\sqrt{0{,}25}=0{,}5 \quad</math> nachdem <math>0{,}5^2 |
| - | = 0{,}5 \cdot 0{,}5 = 0{,}25 </math> | + | = 0{,}5 \cdot 0{,}5 = 0{,}25 </math> und <math>0{,}5</math> eine positive Zahl ist. </li> |
| - | <li><math>\sqrt{2} \approx 1{,}4142 \quad</math> | + | <li><math>\sqrt{2} \approx 1{,}4142 \quad</math> nachdem <math>1{,}4142 |
| - | \cdot 1{,}4142 \approx 2</math> | + | \cdot 1{,}4142 \approx 2</math> und <math>1{,}4142</math> positiv ist. </li> |
| - | <li> | + | <li> Die Gleichung <math>x^2=2</math> hat die Wurzeln (Lösungen) <math>x=\sqrt{2} |
| - | \approx 1{,}414</math> | + | \approx 1{,}414</math> und <math>x = -\sqrt{2} \approx -1{,}414</math>.</li> |
| - | <li><math>\sqrt{-4}\quad</math> | + | <li><math>\sqrt{-4}\quad</math> ist nicht definiert, nachdem es keine reelle Zahl <math>x</math> gibt, die, die Gleichung <math>x^2=-4</math> erfüllt.</li> |
| - | <li><math>\sqrt{(-7)^2} = 7 \quad</math> | + | <li><math>\sqrt{(-7)^2} = 7 \quad</math> nachdem <math> \sqrt{(-7)^2} |
= \sqrt{(-7) \cdot (-7)} = \sqrt{49} = \sqrt{ 7 \cdot 7} = 7</math>.</li> | = \sqrt{(-7) \cdot (-7)} = \sqrt{49} = \sqrt{ 7 \cdot 7} = 7</math>.</li> | ||
</ol> | </ol> | ||
Version vom 13:31, 23. Mär. 2009
| Theorie | Übungen |
Inhalt:
- Square roots and n'th roots
- Manipulating roots
Lernziele:
Nach diesem Abschnitt sollten Sie folgendes können:
- How to calculate the square root of some simple integers.
- That the square root of a negative number has not been defined.
- That the square root of a number denotes the positive root.
- How to manipulate roots in the simplification of expressions containing roots.
- To recognise when the methods of manipulating roots are valid. (Non-negative arguments).
- How to simplify expressions containing quadratic roots in the denominator.
- When the n'th root of a negative number is defined (n odd).
Quadratwurzeln
Der schon bekannte Symbol \displaystyle \sqrt{a}, bezeichnet die Quadratwurzel einer positiven Zahl \displaystyle a, mit anderen Wörtern die wir bekommen wenn wir a mit a multiplizieren. Es gibt aber eine genauere Definition von der Quadratwurzel.
Der Ausdruck \displaystyle x^2 = 4 hat wie bekannt zwei Wurzeln, \displaystyle x = 2 und \displaystyle x = -2, nachdem \displaystyle 2\cdot 2 = 4 und \displaystyle (-2)\cdot(-2) = 4. Desshalb scheint es natürlich dass \displaystyle \sqrt{4} entweder \displaystyle -2 oder \displaystyle 2, also \displaystyle \sqrt{4}= \pm 2. Dies ist aber nicht der Fall, sondern \displaystyle \sqrt{4} bezeichnet nur die Positive Wurzel \displaystyle 2.
Wie Quadratwurzel \displaystyle \sqrt{a} ist die nicht negative Zahl, die mit sich selbst multipliziert \displaystyle a ergibt, also die nicht negative Lösung der Gleichung \displaystyle x^2 = a.
Die Quadratwurzel von \displaystyle a kann auch wie \displaystyle a^{1/2} geschrieben werden.
Deshalb ist es falsch \displaystyle \sqrt{4}= \pm 2, zu schreiben, aber richtig dass die Gleichung \displaystyle x^2 = 4 die Wurzeln (Lösungen) \displaystyle x = \pm 2 hat.
Beispiel 1
- \displaystyle \sqrt{0}=0 \quad nachdem \displaystyle 0^2 = 0 \cdot 0 = 0 und \displaystyle 0 nicht negativ ist.
- \displaystyle \sqrt{100}=10 \quad nachdem \displaystyle 10^2 = 10 \cdot 10 = 100 und \displaystyle 10 eine positive Zahl ist.
- \displaystyle \sqrt{0{,}25}=0{,}5 \quad nachdem \displaystyle 0{,}5^2 = 0{,}5 \cdot 0{,}5 = 0{,}25 und \displaystyle 0{,}5 eine positive Zahl ist.
- \displaystyle \sqrt{2} \approx 1{,}4142 \quad nachdem \displaystyle 1{,}4142 \cdot 1{,}4142 \approx 2 und \displaystyle 1{,}4142 positiv ist.
- Die Gleichung \displaystyle x^2=2 hat die Wurzeln (Lösungen) \displaystyle x=\sqrt{2} \approx 1{,}414 und \displaystyle x = -\sqrt{2} \approx -1{,}414.
- \displaystyle \sqrt{-4}\quad ist nicht definiert, nachdem es keine reelle Zahl \displaystyle x gibt, die, die Gleichung \displaystyle x^2=-4 erfüllt.
- \displaystyle \sqrt{(-7)^2} = 7 \quad nachdem \displaystyle \sqrt{(-7)^2} = \sqrt{(-7) \cdot (-7)} = \sqrt{49} = \sqrt{ 7 \cdot 7} = 7.
When taking square roots, it is useful to know some methods of calculation. As \displaystyle \sqrt{a} = a^{1/2} we can use the laws of exponents as "laws of roots". For example, we have
\displaystyle \sqrt{9\cdot 4}
= (9\cdot 4)^{1/2}
= 9^{1/2}\cdot 4^{1/2}
= \sqrt{9}\cdot \sqrt{4}\mbox{.}
|
In this way we obtain the following rules for quadratic roots, which apply to all real numbers \displaystyle a, b \ge 0:
\displaystyle \begin{align*}
\sqrt{ab} &= \sqrt{\vphantom{b}a}\cdot \sqrt{b}\\[4pt]
\sqrt{\frac{a}{b}} &= \frac{\sqrt{a}}{\sqrt{b}}\\[4pt]
a\sqrt{b} &= \sqrt{a^2b}
\end{align*}
|
( We must however, in the above division, assume as always that b is not 0.)
Beispiel 2
- \displaystyle \sqrt{64\cdot 81} = \sqrt{64}\cdot \sqrt{81} = 8\cdot 9 = 72
- \displaystyle \sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}
- \displaystyle \sqrt{18} \cdot \sqrt{2} = \sqrt{18 \cdot 2} = \sqrt{36} = 6
- \displaystyle \frac{\sqrt{75}}{\sqrt{3}} = \sqrt{\frac{75}{3}} = \sqrt{25} = 5
- \displaystyle \sqrt{12} = \sqrt{ 4 \cdot 3 } = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}
Note that the above calculations assume that \displaystyle a and \displaystyle b \ge 0. If \displaystyle a and \displaystyle b are negative (< 0) then \displaystyle \sqrt{a} and \displaystyle \sqrt{b} are not defined as real numbers. It is tempting to write , for example,
| \displaystyle -1 = \sqrt{-1} \cdot \sqrt{-1} = \sqrt{ (-1) \cdot (-1) } = \sqrt{1} = 1 |
but something here cannot be right. The explanation is that \displaystyle \sqrt{-1} is not a real number, which means the laws of roots discussed above may not be used.
Higher order roots
The cube root of a number \displaystyle a is defined as the number that multiplied by itself three times gives \displaystyle a, and is denoted as \displaystyle \sqrt[\scriptstyle 3]{a}.
Beispiel 3
- \displaystyle \sqrt[\scriptstyle 3]{8} = 2 \quad as \displaystyle 2 \cdot 2 \cdot 2=8.
- \displaystyle \sqrt[\scriptstyle 3]{0{,}027} = 0{,}3 \quad since \displaystyle 0{,}3 \cdot 0{,}3 \cdot 0{,}3 = 0{,}027.
- \displaystyle \sqrt[\scriptstyle 3]{-8} = -2 \quad because \displaystyle (-2) \cdot (-2) \cdot (-2)= -8.
Note that, unlike square roots, cube roots are also defined for negative numbers.
For any positive integers \displaystyle n one can define the \displaystyle n'th root of a number \displaystyle a as
- if \displaystyle n is even and \displaystyle a\ge0 then \displaystyle \sqrt[\scriptstyle n]{a} is the non-negative number that when multiplied by itself \displaystyle n times gives \displaystyle a,
- if \displaystyle n is odd, \displaystyle \sqrt[\scriptstyle n]{a} is the number that when multiplied by itself \displaystyle n times gives \displaystyle a.
The root \displaystyle \sqrt[\scriptstyle n]{a} can also be written as \displaystyle a^{1/n}.
Beispiel 4
- \displaystyle \sqrt[\scriptstyle 4]{625} = 5\quad since \displaystyle 5 \cdot 5 \cdot 5 \cdot 5 = 625.
- \displaystyle \sqrt[\scriptstyle 5]{-243} = -3\quad because \displaystyle (-3) \cdot (-3) \cdot (-3) \cdot (-3) \cdot (-3) = -243.
- \displaystyle \sqrt[\scriptstyle 6]{-17}\quad is not defined as \displaystyle 6 is even and \displaystyle -17 is a negative number.
For \displaystyle n'th roots the same rules apply as for quadratic roots if \displaystyle a, \, b \ge 0. Note that if \displaystyle n is odd these methods apply even for negative \displaystyle a and \displaystyle b, that is, for all real numbers \displaystyle a and \displaystyle b.
\displaystyle \begin{align*}
\sqrt[\scriptstyle n]{ab}
&= \sqrt[\scriptstyle n]{\vphantom{b}a}\cdot
\sqrt[\scriptstyle n]{b}\\[4pt]
\sqrt[\scriptstyle n]{\frac{a}{b}}
&= \frac{\sqrt[\scriptstyle n]{a}}{\sqrt[\scriptstyle n]{b}}\\[4pt]
a\,\sqrt[\scriptstyle n]{b}
&= \sqrt[\scriptstyle n]{a^nb}
\end{align*}
|
Simplification of expressions containing roots
Often, one can significantly simplify expressions containing roots by using the usual methods for roots . As is also the case when using the laws of exponents, it is desirable to reduce expressions into as "small" roots as possible. For example, it is a good idea to do the following
\displaystyle \sqrt{8}
= \sqrt{4\cdot2}
= \sqrt{4} \cdot \sqrt{2}
= 2\sqrt{2}
|
because it helps simplification as we see here
\displaystyle \frac{\sqrt{8}}{2}
= \frac{2 \sqrt{2}}{2}
= \sqrt{2}\mbox{.}
|
By rewriting expressions containing roots in terms of "small" roots one can also sum roots of "the same kind", e.g.
\displaystyle \sqrt{8} + \sqrt{2}
= 2\sqrt{2} + \sqrt{2}
= (2+1)\sqrt{2}
= 3\sqrt{2}\mbox{.}
|
Beispiel 5
- \displaystyle \frac{\sqrt{8}}{\sqrt{18}} = \frac{\sqrt{2 \cdot 4}}{\sqrt{2 \cdot 9}} = \frac{\sqrt{2 \cdot 2 \cdot 2}}{\sqrt{2 \cdot 3 \cdot 3}} = \frac{\sqrt{2 \cdot 2^2}}{\sqrt{2 \cdot 3^2}} = \frac{2\sqrt{2}}{3\sqrt{2}} = \frac{2}{3}
- \displaystyle \frac{\sqrt{72}}{6} = \frac{\sqrt{8 \cdot 9}}{ 2 \cdot 3} = \frac{\sqrt{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3}}{ 2 \cdot 3} = \frac{\sqrt{2^2 \cdot 3^2 \cdot 2}}{ 2 \cdot 3} = \frac{2 \cdot 3\sqrt{2}}{2 \cdot 3} = \sqrt{2}
- \displaystyle \sqrt{45} + \sqrt{20}
= \sqrt{9\cdot5} + \sqrt{4\cdot5}
= \sqrt{3^2\cdot5} + \sqrt{2^2\cdot5}
= 3\sqrt{5} + 2\sqrt{5}\vphantom{\bigl(}
\displaystyle \phantom{\sqrt{45} + \sqrt{20}\vphantom{\bigl(}}{} = (3+2)\sqrt{5} = 5\sqrt{5} - \displaystyle \sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}
= \sqrt{5 \cdot 10} + 2\sqrt{3} -\sqrt{2 \cdot 16}
+ \sqrt{3 \cdot 9}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{5 \cdot 2 \cdot 5} + 2\sqrt{3} -\sqrt{2 \cdot 4 \cdot 4} + \sqrt{3 \cdot 3 \cdot 3}\vphantom{a^{b^c}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{5^2 \cdot 2 } + 2\sqrt{3} -\sqrt{2^2 \cdot 2^2 \cdot 2} + \sqrt{3 \cdot 3^2}\vphantom{a^{\textstyle b^{\textstyle c}}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = 5\sqrt{2} +2\sqrt{3} - 2 \cdot 2\sqrt{2} + 3\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = (5-4)\sqrt{2} + (2+3)\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}}
\displaystyle \phantom{\sqrt{50} + 2\sqrt{3} -\sqrt{32} + \sqrt{27}\vphantom{\Bigl(}}{} = \sqrt{2} + 5\sqrt{3}\vphantom{a^{\textstyle b^{\textstyle c}}} - \displaystyle \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{12} } = \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{3 \cdot 4} } = \frac{ 2\cdot\sqrt[\scriptstyle3]{3} }{ \sqrt[\scriptstyle3]{3} \cdot \sqrt[\scriptstyle3]{4} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{4} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{2 \cdot 2} } = \frac{ 2 }{ \sqrt[\scriptstyle3]{2} \cdot \sqrt[\scriptstyle3]{2} } \cdot \displaystyle \frac{\sqrt[\scriptstyle3]{2}}{ \sqrt[\scriptstyle3]{2}} = \frac{ 2\cdot\sqrt[\scriptstyle3]{2} }{ 2 } = \sqrt[\scriptstyle3]{2}
- \displaystyle (\sqrt{3} + \sqrt{2}\,)(\sqrt{3} - \sqrt{2}\,) = (\sqrt{3}\,)^2-(\sqrt{2}\,)^2 = 3-2 = 1 where we have used the difference of two squares \displaystyle (a+b)(a-b) = a^2 - b^2 with \displaystyle a=\sqrt{3} and \displaystyle b=\sqrt{2}.
Rational root expressions
When roots appear in a rational expression one often wants to avoid roots in the denominator (because it is difficult with hand calculations to divide by irrational numbers). By multiplying the numerator and denominator by \displaystyle \sqrt{2} for example, one obtains
\displaystyle \frac{1}{\sqrt{2}}
= \frac{1\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}
= \frac{\sqrt{2}}{2}
|
which usually is preferable.
In other cases, you can take advantage of the difference of two squares method, \displaystyle (a+b)(a-b) = a^2 – b^2. One multiplies the numerator and denominator by the denominator´s “conjugate” expression and the root sign is eliminated from the denominator by squaring, as in the following,
\displaystyle \begin{align*}
\frac{\sqrt{3}}{\sqrt{2}+1}
&= \frac{\sqrt{3}}{\sqrt{2}+1} \cdot \frac{\sqrt{2}-1}{\sqrt{2}-1}
= \frac{\sqrt{3}\,(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}\\[4pt]
&= \frac{\sqrt{3}\cdot\sqrt{2} - \sqrt{3}\cdot1}{(\sqrt{2}\,)^2 - 1^2 }
= \frac{\sqrt{3 \cdot 2} - \sqrt{3}}{ 2 - 1 }
= \frac{\sqrt{6} - \sqrt{3}}{ 1 }
= \sqrt{6} - \sqrt{3}\mbox{.}
\end{align*}
|
Beispiel 6
- \displaystyle \frac{10\sqrt{3}}{\sqrt{5}} = \frac{10\sqrt{3}\cdot\sqrt{5}}{\sqrt{5}\cdot\sqrt{5}} = \frac{10\sqrt{15}}{5} = 2\sqrt{15}
- \displaystyle \frac{1+\sqrt{3}}{\sqrt{2}} = \frac{(1+\sqrt{3})\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} = \frac{\sqrt{2}+\sqrt{6}}{2}
- \displaystyle \frac{3}{\sqrt{2}-2} = \frac{3(\sqrt{2}+2)}{(\sqrt{2}-2)(\sqrt{2}+2)} = \frac{3\sqrt{2}+6}{(\sqrt{2}\,)^2-2^2} = \frac{3\sqrt{2}+6}{2-4} = -\frac{3\sqrt{2}+6}{2}
- \displaystyle \frac{\sqrt{2}}{\sqrt{6}+\sqrt{3}}
= \frac{\sqrt{2}\,(\sqrt{6}-\sqrt{3}\,)}{(\sqrt{6}+\sqrt{3}\,)
(\sqrt{6}-\sqrt{3}\,)}
= \frac{\sqrt{2}\,\sqrt{6}-\sqrt{2}\,\sqrt{3}}{(\sqrt{6}\,)^2
-(\sqrt{3}\,)^2}\vphantom{\Biggl(}
\displaystyle \phantom{\frac{\sqrt{2}}{\sqrt{6}+\sqrt{3}}\vphantom{\Biggl(}}{} = \frac{\sqrt{2}\,\sqrt{2\cdot 3}-\sqrt{2}\,\sqrt{3}}{6-3} = \frac{2\sqrt{3}-\sqrt{2}\,\sqrt{3}}{3} = \frac{(2-\sqrt{2}\,)\sqrt{3}}{3} \vphantom{\displaystyle\frac{a^{\textstyle b^{\textstyle c}}}{b}}
Tipps fürs lernen
Diagnostische Prüfung und Schlussprüfung
Nachdem Du fertig mit der Theorie bist, sollst Du die diagnostische Prüfung und die Schlussprüfung machen. Du findest die links zu den Prüfungen in Deiner "Student Lounge".
Bedenke folgendes:
The square root of a number is always non-negative (that is, positive or zero)!
Rules for roots are actually a special case of laws of exponents .
For example: \displaystyle \sqrt{x}=x^{1/2}.
Reviews
For those of you who want to deepen your studies or need more detailed explanations consider the following references
Learn more about square roots in the English Wikipedia
How do we know that the root of 2 is not a fraction?
Nützliche Websites
How to find the root of a number, without the help of calculators?