Lösung 4.1:5a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
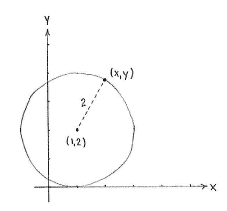
A circle is defined as all the points which have a fixed distance to the circle's midpoint. Hence, a point (''x'',''y'') lies on our circle if and only if its distance to the point (1,3) is exactly 2. Using the distance formula, we can express this condition as
-
[[Image:4_1_5_a.gif|center]]
+
-
{{NAVCONTENT_STOP}}
+
{{Displayed math||<math>\sqrt{(x-1)^2 + (y-2)^2} = 2\,\textrm{.}</math>}}
 +
After squaring, we obtain the equation of the circle in standard form,
-
A circle is defined as all the points which have a fixed distance to the circle's midpoint. Hence, a point
+
{{Displayed math||<math>(x-1)^2 + (y-2)^2 = 4\,\textrm{.}</math>}}
-
<math>\left( x \right.,\left. y \right)</math>
+
-
lies on our circle if and only if its distance to the point
+
-
<math>\left( 1 \right.,\left. 3 \right)</math>
+
-
is exactly
+
-
<math>2</math>. Using the distance formula, we can express this condition as
+
-
<math>\sqrt{\left( x-1 \right)^{2}+\left( y-2 \right)^{2}}=2</math>
+
[[Image:4_1_5_a.gif|center]]
-
 
+
-
 
+
-
After squaring, we obtain the equation of the circle in standard form:
+
-
 
+
-
 
+
-
<math>\left( x-1 \right)^{2}+\left( y-2 \right)^{2}=4</math>
+

Version vom 10:47, 7. Okt. 2008

A circle is defined as all the points which have a fixed distance to the circle's midpoint. Hence, a point (x,y) lies on our circle if and only if its distance to the point (1,3) is exactly 2. Using the distance formula, we can express this condition as

Vorlage:Displayed math

After squaring, we obtain the equation of the circle in standard form,

Vorlage:Displayed math


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.1:5a“