Lösung 4.4:2d

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 4.4:2d moved to Solution 4.4:2d: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
Apart from the fact that there is a
-
<center> [[Image:4_4_2d-1(2).gif]] </center>
+
<math>\text{5}x</math>, this is a normal trigonometric equation of the type
-
{{NAVCONTENT_STOP}}
+
<math>\text{sin }y\text{ }=a</math> . If we are only interested in solutions which satisfy
-
{{NAVCONTENT_START}}
+
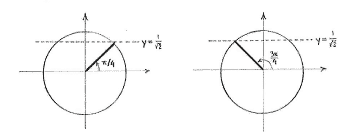
<math>0\le \text{5}x\le \text{2}\pi </math>, then a sketch of the unit circle shows that there are two such solutions,
-
<center> [[Image:4_4_2d-2(2).gif]] </center>
+
<math>\text{5}x=\text{ }\frac{\pi }{4}</math>
-
{{NAVCONTENT_STOP}}
+
and the reflectionally symmetric solution
 +
<math>\text{5}x=\text{ }\pi \text{-}\frac{\pi }{4}=\frac{3\pi }{4}</math>.
 +
 
[[Image:4_4_2_d.gif|center]]
[[Image:4_4_2_d.gif|center]]
 +
 +
All of the equation's solutions are obtained from all values of 5x which differ by a multiple of 2π from either of these two solutions:
 +
 +
 +
<math>\text{5}x=\text{ }\frac{\pi }{4}+2n\pi </math>
 +
and
 +
<math>\text{5}x=\frac{3\pi }{4}+2n\pi </math>,
 +
 +
where
 +
<math>n</math>
 +
is an arbitrary integer.
 +
 +
If we divide both of these by
 +
<math>\text{5}</math>, we obtain the solutions expressed in terms of x alone:
 +
 +
 +
<math>x=\frac{\pi }{20}+\frac{2}{5}n\pi </math>
 +
and
 +
<math>x=\frac{3\pi }{20}+\frac{2}{5}n\pi </math>,
 +
 +
where
 +
<math>n</math>
 +
is an arbitrary integer.

Version vom 13:55, 30. Sep. 2008

Apart from the fact that there is a \displaystyle \text{5}x, this is a normal trigonometric equation of the type \displaystyle \text{sin }y\text{ }=a . If we are only interested in solutions which satisfy \displaystyle 0\le \text{5}x\le \text{2}\pi , then a sketch of the unit circle shows that there are two such solutions, \displaystyle \text{5}x=\text{ }\frac{\pi }{4} and the reflectionally symmetric solution \displaystyle \text{5}x=\text{ }\pi \text{-}\frac{\pi }{4}=\frac{3\pi }{4}.


All of the equation's solutions are obtained from all values of 5x which differ by a multiple of 2π from either of these two solutions:


\displaystyle \text{5}x=\text{ }\frac{\pi }{4}+2n\pi and \displaystyle \text{5}x=\frac{3\pi }{4}+2n\pi ,

where \displaystyle n is an arbitrary integer.

If we divide both of these by \displaystyle \text{5}, we obtain the solutions expressed in terms of x alone:


\displaystyle x=\frac{\pi }{20}+\frac{2}{5}n\pi and \displaystyle x=\frac{3\pi }{20}+\frac{2}{5}n\pi ,

where \displaystyle n is an arbitrary integer.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:2d“