Lösung 4.4:2d
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 5: | Zeile 5: | ||
All of the equation's solutions are obtained from all values of <math>5x</math> which differ by a multiple of <math>2\pi</math> from either of these two solutions, | All of the equation's solutions are obtained from all values of <math>5x</math> which differ by a multiple of <math>2\pi</math> from either of these two solutions, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>5x = \frac{\pi}{4} + 2n\pi\qquad\text{and}\qquad 5x = \frac{3\pi}{4} + 2n\pi\,,</math>}} |
where ''n'' is an arbitrary integer. | where ''n'' is an arbitrary integer. | ||
| Zeile 11: | Zeile 11: | ||
If we divide both of these by 5, we obtain the solutions expressed in terms of ''x'' alone, | If we divide both of these by 5, we obtain the solutions expressed in terms of ''x'' alone, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>x = \frac{\pi}{20} + \frac{2}{5}n\pi\qquad\text{and}\qquad x = \frac{3\pi}{20} + \frac{2}{5}n\pi\,,</math>}} |
where ''n'' is an arbitrary integer. | where ''n'' is an arbitrary integer. | ||
Version vom 08:58, 22. Okt. 2008
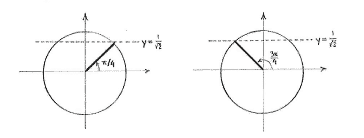
Apart from the fact that there is a \displaystyle 5x, this is a normal trigonometric equation of the type \displaystyle \sin y = a\,. If we are only interested in solutions which satisfy \displaystyle 0\le 5x\le 2\pi, then a sketch of the unit circle shows that there are two such solutions, \displaystyle 5x = \pi/4 and the reflectionally symmetric solution \displaystyle 5x = \pi - \pi/4 = 3\pi/4\,.
All of the equation's solutions are obtained from all values of \displaystyle 5x which differ by a multiple of \displaystyle 2\pi from either of these two solutions,
| \displaystyle 5x = \frac{\pi}{4} + 2n\pi\qquad\text{and}\qquad 5x = \frac{3\pi}{4} + 2n\pi\,, |
where n is an arbitrary integer.
If we divide both of these by 5, we obtain the solutions expressed in terms of x alone,
| \displaystyle x = \frac{\pi}{20} + \frac{2}{5}n\pi\qquad\text{and}\qquad x = \frac{3\pi}{20} + \frac{2}{5}n\pi\,, |
where n is an arbitrary integer.