Lösung 4.3:1c
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
| Zeile 7: | Zeile 7: | ||
-axis. | -axis. | ||
| - | + | ||
| - | < | + | |
| - | + | <center> [[Image:4_3_1_c.gif]] </center> | |
| + | |||
| + | slope = | ||
<math>{\tan 2\pi }/{7}\;</math> | <math>{\tan 2\pi }/{7}\;</math> | ||
| - | FIGURE2 | ||
From the figure, we see that the angle between | From the figure, we see that the angle between | ||
| Zeile 20: | Zeile 21: | ||
<math>{2\pi }/{7}\;</math> | <math>{2\pi }/{7}\;</math> | ||
is | is | ||
| - | <math>{v=2\pi }/{7}\;+\pi ={9\pi }/{7}\;</math> | + | <math>{v=2\pi }/{7}\;+\pi ={9\pi }/{7}\;</math>. |
| - | . | + | |
Version vom 10:19, 29. Sep. 2008
The tangent value of the angle \displaystyle {2\pi }/{7}\; is the gradient of the line which makes an angle \displaystyle {2\pi }/{7}\; with the \displaystyle x -axis.
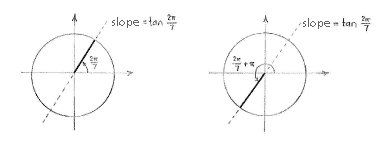
slope = \displaystyle {\tan 2\pi }/{7}\;
From the figure, we see that the angle between \displaystyle {\pi }/{2}\; and \displaystyle 2\pi which gives a line with the same slope as the angle \displaystyle {2\pi }/{7}\; is \displaystyle {v=2\pi }/{7}\;+\pi ={9\pi }/{7}\;.
